Conv1d与Conv2d
本文分为几个部分来详解Conv2d与Conv1d。主要侧重于Conv2d
前言
本文记于2020年12月15日,起因是DGCNN中部分卷积使用了二维卷积,部分卷积使用了一维卷积。加之之前对Conv2d与Conv1d属于一种迷迷糊糊的状态,趁着这个机会弄清楚。
Conv2d原理(二维卷积层)
二维互相关运算
互相关运算与卷积运算
虽然卷积层得名于卷积(convolution)运算,但所有框架在实现卷积层的底层,都采用的是互相关运算。实际上,卷积运算与互相关运算类似,为了得到卷积运算的输出,我们只需要将核数组左右翻转并上下翻转,然后再与输入数组做互相关运算。所以这两种运算虽然类似,但是输出并不相同。
但是由于深度学习中核数组都是学习得到的,所以卷积层无论使用互相关运算还是卷积运算,都不影响模型预测时的输出。也就是说我们用卷积运算学出的核数组与用互相关运算学出的核数组两者之间可以通过上下翻转,左右翻转来相互转换。所以在框架乃至于绝大部分深度学习文献中,都使用互相关运算来代替了卷积运算。
互相关运算
在二维卷积层中,一个二维输入数组和一个二维核(kernel)数组通过互相关运算输出一个二维数组。举个例子来解释二维互相关运算:
假设输入数组的高和宽均为3, 核数组的高和宽均为2,该数组在卷积运算中又称为卷积核或者过滤器(filter)。
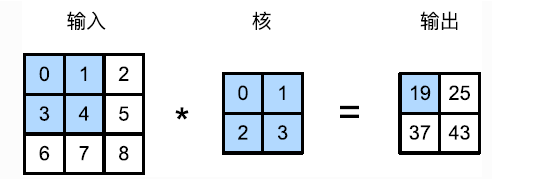
19是这样得出的: $19 = 0\times0 + 1\times1 + 3\times2 + 4\times3$ 。
卷积窗口从输入数组的最左上方开始,按照从左往右,从上往下的顺序,依次在输入数组上滑动。当卷积窗口滑动到某一位置时,窗口中的输入子数组与核数组按元素相乘并求和。得到输出数组中对应位置的元素。
二维卷积层
二维卷积层将输入和卷积核做互相关运算,并加上一个标量偏差来得到输出。卷积层的模型参数包含了卷积核和标量偏差。我们在训练模型的时候,通常先对卷积层进行随机的初始化,然后不断迭代卷积核和偏差。
卷积窗口形状为$p \times q$的卷积层称为$p \times q$卷积层。
特征图与感受野
二维卷积层输出的二维数组可以看做是输入在空间维度上(宽和高)上某一级的表征,也叫特征图(feature map)。影响元素$x$的前向计算的所有可能输入区域(甚至可能大于输入的实际尺寸)叫做$x$的感受野(receptive field)。以上图为例,图中输入的阴影部分的四个元素就是输出数组中阴影部分元素的感受野。如果我们将该输出再和一个$2 \times 2$的核数组做互相关运算,输出单个元素$z$。那么$z$在输入上的感受野包含全部的9个元素。
可见,我们可以通过更深的卷积神经网络使特征图中单个元素的感受野变得更加广阔,从而捕捉输入上更大尺寸的特征。
填充与步幅
卷积层的输出形状由输入形状和卷积核窗口形状决定,通过填充与步幅,我们可以改变给定形状的输入和卷积层下的输出形状。
填充
填充padding是指在输入高和宽的两侧填充元素(通常是0元素)。如下图:
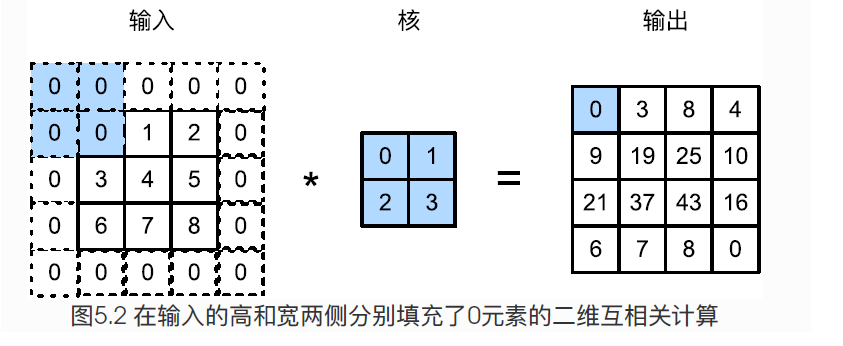
假设输入形状为$n_h \times n_w$, 卷积核窗口形状是$k_h \times k_w$,在高的两侧一共填充$p_h$行,在宽的两侧一共填充$p_w$列,那么输出形状将会是: $$ (n_h - k_h + p_h + 1) \times (n_w - k_w + p_w + 1) $$ 很多情况下我们会设置$p_h = k_h -1$和$p_w = k_w - 1$来使得输入输出具有相同的高和宽。
对于任意的二维数组X,当两端的填充个数相同,并使得输入和输出具有相同的高和宽时,我们就知道输出Y[i,j]是输入以X[i,j]为中心的窗口同卷积核进行互相关运算而得到的。
步幅
卷积窗口从输入数组的最左上方开始,按照从左向右,从上向下的顺序,依次在输入数组上滑动。我们将每次滑动的行数和列数称为步幅(stride)。
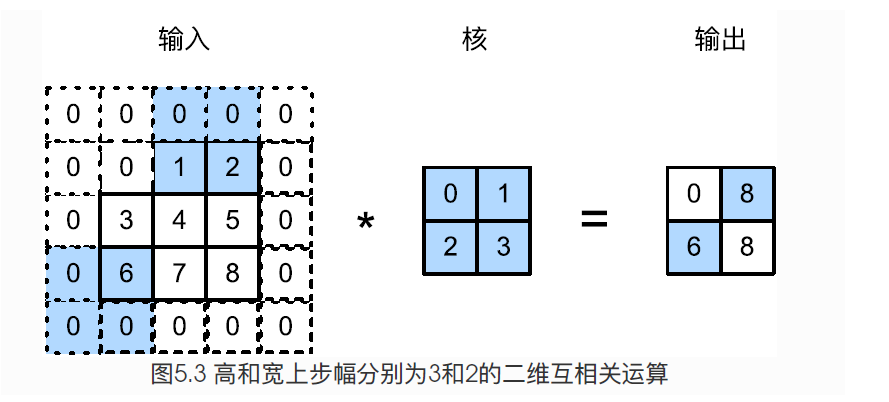
当高上步幅为$s_h$,宽上步幅为$s_w$时,输出形状为: $$ [(n_h - k_h + p_h + s_h)/s_h] \times [(n_w - k_w +p_w +s_w) / s_w] $$
为了表述简洁,当输入的高和宽两侧的填充数分别为$p_h$和$p_w$时,我们称填充为$(p_h, p_w)$。特别地,当$p_h = p_w = p$时,填充为$p$。当在高和宽上的步幅分别为$s_h$和$s_w$时,我们称步幅为($s_h,s_w$)。特别地,当$s_h = s_w = s$时,步幅为$s$。在默认情况下,填充为0,步幅为1.
多输入通道和多输出通道
多输入通道
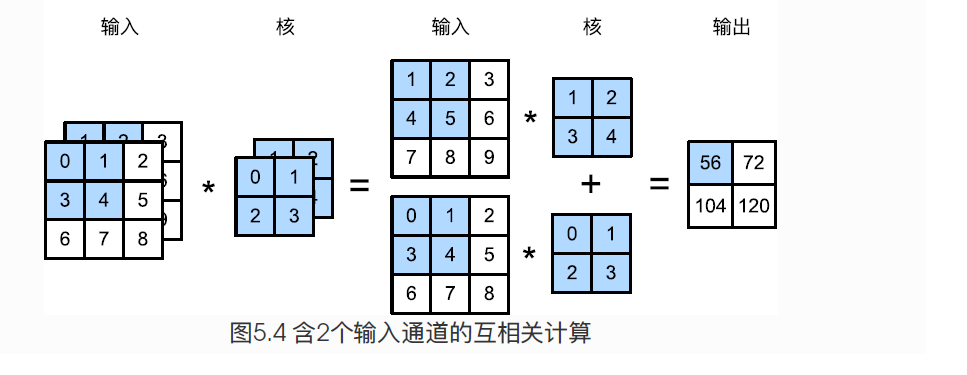
当输入数据含多个通道时,我们需要构造一个输入通道数和输入数据的通道数相同的卷积核,从而能够与含多通道的输入数据做互相关运算。
假设输入数据的通道数为$c_i$,那么卷积核的输入通道数同样为$c_i$。设卷积核的窗口形状为$k_h \times k_w$。当$c_i = 1$,我们知道卷积核只包含一个形状为$k_h \times k_w$的二维数组。当$c_i > 1$时,我们将会为每个输入通道各分配一个形状为$k_h \times k_w$的核数组,这$c_i$个数组在通道维上连结,即得到一个形状为$c_i \times k_h \times k_w$的卷积核。
由于输入和卷积核各有$c_i$个通道,我们可以在各个通道上对输入的二维数组和卷积核的二维核数组做互相关运算,再将这$c_i$个互相关运算的二维输出按照通道相加,得到一个二维数组。 这就是多个通道的输入数据与多输入通道的卷积核做二维互相关运算的输出。
多输出通道
当输入通道有多个时,因为我们对各个通道的结果进行了累加,所以不论输入通道数是多少,输出通道数总是为1。 设卷积核输入通道数和输出通道数分别为$c_i$和$c_o$,宽和高分别为$k_h$和$k_w$。如果希望得到含多个通道的输出,我们可以为每个输出通道分别创建形状为$c_i \times k_h \times k_w$的核数组。将它们在输出通道维连结,卷积核的形状即:$c_o \times c_i \times k_h \times k_w$。 在做互相关运算时,每个输出通道上的结果由卷积核在该输出通道上的核数组与整个输入数组计算而来。
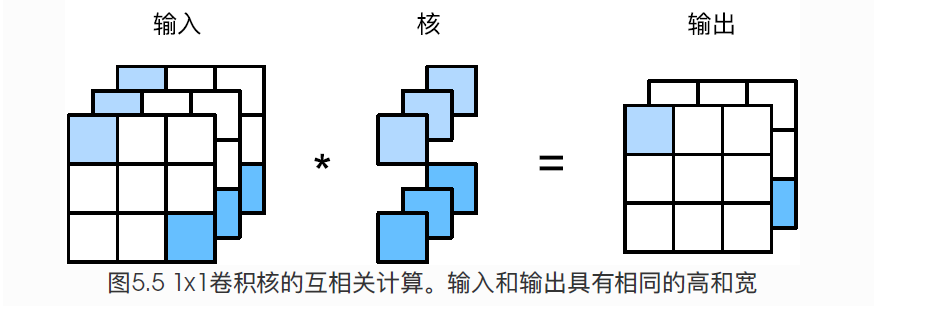
$1 \times 1$卷积层 与 全连接层
最后我们讨论卷积窗口形状为$1 \times 1 (k_h = k_w =1)$的多通道卷积层。我们通常称之为$1\times1$卷积层,并将其中的卷积运算称为$1\times1$卷积。因为使用了最小窗口,$1\times1$卷积失去了卷积层可以识别高和宽维度上相邻元素构成的模式的功能。实际上,$1\times1$卷积的主要计算发生在通道维上。$1\times1$卷积的输入和输出具有相同的高和宽。输出中的每个元素来自于输入中在高和宽上相同位置的元素在不同通道之间按权重累加。假设我们将通道维当做特征维,而将高和宽维度上的元素当成数据样本,那么$1\times1$卷积层的作用于全连接层等价。
用$1\times1$卷积替代全连接层的时候,一定需要注意Tensor的维度顺序。
Conv1d
Conv1d的输入是三维数据:(Batch_size, channels, width)
卷积操作沿着通道维对width维进行。