DCP论文阅读笔记
论文
Deep Closest Point: Learning Representations for Point Cloud Registration
Author: Wang, Yue; Solomon, Justin
Main Attribution
基于ICP迭代最近点算法,提出基于深度学习的DCP算法。解决了ICP想要采用深度学习方法时遇到的一系列问题。
我们先回顾一下ICP算法的基本步骤:
for each iteration:
find corresponding relations of points between two scan(using KNN)
using SVD to solve Rotation Matrix and Translation vector
update cloud Data
概括起来就是: 寻找最近点对关系,使用SVD求解刚体变换。如此循环往复。
结合论文,个人理解将ICP算法扩展到深度学习存在着以下的难点(可能存在各种问题,笔者深度学习的相关知识很薄弱):
- 首先,点对关系如果是确定的话,沿着网络反向传播可能存在问题。
- SVD分解求解刚体变换,如何求梯度?(Confirmed by paper)
而文章克服了这些问题,主要有如下贡献:
- 提出了能够解决传统ICP算法试图推广时存在的困难的一系列子网络架构。
- 提出了能进行
pair-wise配准的网络架构 - 评估了在采用不同设置的情况下的网络表现
- 分析了是
global feature有用还是local feature对配准更加有用
网络架构

模型包含三个部分:
(1) 一个将输入点云映射到高维空间embedding的模块,具有扰动不变性(指DGCNN当点云输入时点的前后顺序发生变化,输出不会有任何改变) 或者 刚体变换不变性(指PointNet对于旋转平移具有不变的特性)。该模块的作用是寻找两个输入点云之间的点的对应关系. 可选的模块有PointNet(Focus于全局特征), DGCNN(结合局部特征和全局特征)。
(2) 一个基于注意力attention的Pointer网络模块,用于预测两个点云之间的soft matching关系(类似于一种基于概率的soft match,之所以soft是由于它并没有显式规定点$x_i$必须与哪个点$x_j$有对应关系,而是通过一个softmax得到的各点和某点$x_i$存在对应关系的概率乘以各点数据,得到一个类似于概率的对应点坐标。 该模块采用的是Transformer
(3) 一个可微的SVD分解层,用于输出刚体变换矩阵。
问题阐述
熟悉点云配准的同学应该知道,问题十分清晰。这里直接粘一下原文。


值得一提的是,作者分析了一下ICP的算法步骤。和我们上面描述的一样。就是用上次更新后的信息寻找最近关系,然后用寻找到的对应关系SVD求解得到$R,t$. 所以如果初始值一开始生成的是很差的corresponding relation,那么一下就会陷入局部最优。
而作者的思路就是:使用学习的网络来得到特征,通过特征获得一个更好的对应关系$m(\cdot)$,用这个$m(\cdot)$去计算刚体变换信息。
代码分析与对应模块详解
我们采用一种Top-Down的视角来分析整个代码。先从整体入手,然后逐渐拆解模块进行分析。
整体模块
DCP网络结构分为三个Part,从代码中就可以很清晰的看出来:第一个Module模块emd_nn用于抽象特征,第二个Module模块pointer用于match,第三个Module模块head用于求解刚体变换矩阵,具体代码如下:
class DCP(nn.Module):
def __init__(self, args): # args 是一个存放各种参数的namespace
super(DCP,self).__init__()
self.emb_dims = args.embdims # 欲抽象到的特征维度,default为 512
self.cycle = args.cycle # ba的刚体变换关系是否重新进入网络计算
if args.emb_nn == 'pointnet': # emb_nn就是上文所说的第一个模块,若选择PointNet
self.emb_nn = PointNet(emb_dims=self.emb_dims)
elif args.emb_nn == 'dgcnn': # 若选择DGCNN
self.emb_nn = DGCNN(emb_dims=self.emb_dims)
else:
raise Exception('Not implemented') # 其他网络尚未实现
if args.pointer == 'identity': # 不使用Transformer, hard match
self.pointer = Identity()
elif args.pointer == 'transformer': # soft matching by tranformer
self.pointer = Transformer(args = args)
else:
raise Exception('Not implemented')
if args.head == 'mlp': # 直接用MLP预测输出矩阵
self.head = MLPHead(args=args)
elif args.head == 'svd': # 使用可微的SVD分解层
self.head = SVDHead(args=args)
else:
raise Exception("Not implemented")
def forward(self, *input):
src = input[0]
tgt = input[1]
src_embedding = self.emb_nn(src)
tgt_embedding = self.emb_nn(tgt) # Module Part 1 (batch_size, emb_dims, num_points)
src_embedding_p, tgt_embedding_p = self.pointer(src_embedding, tgt_embedding) # Module Part 2
src_embedding = src_embedding + src_embedding_p
tgt_embedding = tgt_embedding + tgt_embedding_p
rotation_ab, translation_ab = self.head(src_embedding, tgt_embedding, src, tgt) # Module Part 3
if self.cycle:
rotation_ba, translation_ba = self.head(tgt_embedding, src_embedding, tgt, src)
else:
rotation_ba = rotation_ab.transpose(2,1).contiguous()
translation_ba = -torch.matmul(rotation_ba, translation_ab.unsqueeze(2)).squeeze(2)
return rotation_ab, translation_ab, rotation_ba, translation_ba
用于抽象feature的Module1:emb_nn
考虑emb_nn,我们有两个选择: 其一是PointNet, 其二是DGCNN.
PointNet抽象的特征是global feature, 而DGCNN结合了local feature和global feature.
我们希望得到的是对每一个点抽象而得的特征(即每一个点都有其embedding),并利用两个点云之间点的embedding来生成映射关系(即Match关系). 所以我们要得到的是per-point feature而不是one feature per cloud。
出于上述原因,我们在最后一层的聚合函数aggregation function之前生成每个点的representation。
$$
F_X = {x_1^L,x_2^L, …, x_i^L,…,x_N^L}
$$
$$
F_Y = {y_1^L, y_2^L, …, y_i^L, …, y_N^L}
$$
上标L代表第L层的输出(假定共有L层)。
PointNet
$x_i^l$是第$i$个点在第$l$层后的embedding,而$h_{\theta}^l$是第$l$层的非线性映射函数。PointNet的forward mechanism可以用如下公式给出:
$$
x_i^l = h_{\theta}^l(x_i^{l-1})
$$
作者@WangYue在github上公布的代码,使用的PointNet的网络架构如下:
class PointNet(nn.Module):
def __init__(self, emb_dims=512):
super(PointNet, self).__init__()
self.conv1 = nn.Conv1d(3, 64, kernel_size=1, bias=False)
self.conv2 = nn.Conv1d(64, 64, kernel_size=1, bias=False)
self.conv3 = nn.Conv1d(64, 64, kernel_size=1, bias=False)
self.conv4 = nn.Conv1d(64, 128, kernel_size=1, bias=False)
self.conv5 = nn.Conv1d(128, emb_dims, kernel_size=1, bias=False)
self.bn1 = nn.BatchNorm1d(64)
self.bn2 = nn.BatchNorm1d(64)
self.bn3 = nn.BatchNorm1d(64)
self.bn4 = nn.BatchNorm1d(128)
self.bn5 = nn.BatchNorm1d(emb_dims)
def forward(self, x):
x = F.relu(self.bn1(self.conv1(x)))
x = F.relu(self.bn2(self.conv2(x)))
x = F.relu(self.bn3(self.conv3(x)))
x = F.relu(self.bn4(self.conv4(x)))
x = F.relu(self.bn5(self.conv5(x)))
return x
从上述代码中,可以看出,作者使用的PointNet并没有input-transform和feature-transform这两个Module,相当于只应用MLP不断对输入点云进行抽象,直到高维空间。

存疑:为什么不加Transform-Net? 如果加上效果训练效果如何? 没有cat,cat之后效果如何?
解答:记于2020-12-28日:这个问题太傻了。我们这个网络的目的就是学习出刚体变换矩阵。3x3的Transform Net相当于是硬学。而我们是通过其巧妙设计来优化模式,求解刚体变换矩阵。
DGCNN
DGCNN是作者@WangYue提出的一种网络架构,其特点是EdgeConv。可以结合全局特征与局部特征。
$$
x_i^l = f({{} h_{\theta}^l(x_i^{l-1},x_j^{l-1}); \forall j \in N_i {}})
$$
$f$是每一层后的聚合函数。$N_i$指的是和点$x_i$存在KNN关系的点的集合。
get_graph_feature是返回egde-feature的函数。这并不是我们关注的重点,代码简要粘贴一下。
def knn(x, k):
inner = -2 * torch.matmul(x.transpose(2, 1).contiguous(), x)
xx = torch.sum(x ** 2, dim=1, keepdim=True)
pairwise_distance = -xx - inner - xx.transpose(2, 1).contiguous()
idx = pairwise_distance.topk(k=k, dim=-1)[1] # (batch_size, num_points, k)
return idx
def get_graph_feature(x, k=20):
# x = x.squeeze()
idx = knn(x, k=k) # (batch_size, num_points, k)
batch_size, num_points, _ = idx.size()
device = torch.device('cuda')
idx_base = torch.arange(0, batch_size, device=device).view(-1, 1, 1) * num_points
idx = idx + idx_base
idx = idx.view(-1)
_, num_dims, _ = x.size()
x = x.transpose(2,
1).contiguous() # (batch_size, num_points, num_dims) -> (batch_size*num_points, num_dims) # batch_size * num_points * k + range(0, batch_size*num_points)
feature = x.view(batch_size * num_points, -1)[idx, :]
feature = feature.view(batch_size, num_points, k, num_dims)
x = x.view(batch_size, num_points, 1, num_dims).repeat(1, 1, k, 1)
feature = torch.cat((feature, x), dim=3).permute(0, 3, 1, 2)
return feature
而网络中使用的DGCNN代码如下:
class DGCNN(nn.Module):
def __init__(self, emb_dims=512):
super(DGCNN, self).__init__()
self.conv1 = nn.Conv2d(6, 64, kernel_size=1, bias=False)
self.conv2 = nn.Conv2d(64, 64, kernel_size=1, bias=False)
self.conv3 = nn.Conv2d(64, 128, kernel_size=1, bias=False)
self.conv4 = nn.Conv2d(128,256, kernel_size=1, bias=False)
self.conv5 = nn.Conv2d(512, emb_dims, kernel_size=1, bias=False)
self.bn1 = nn.BatchNorm2d(64)
self.bn2 = nn.BatchNorm2d(64)
self.bn3 = nn.BatchNorm2d(128)
self.bn4 = nn.BatchNorm2d(256)
self.bn5 = nn.BatchNorm2d(emb_dims)
def forward(self,x):
batch_size, num_dims, num_points = x.size()
x = get_graph_feature(x)
x = F.relu(self.bn1(self.conv1(x)))
x1 = x.max(dim=-1, keepdim=True)[0]
x = F.relu(self.bn2(self.conv2(x)))
x2 = x.max(dim=-1, keepdim=True)[0]
x = F.relu(self.bn3(self.conv3(x)))
x3 = x.max(dim=-1, keepdim=True)[0]
x = F.relu(self.bn4(self.conv4(x)))
x4 = x.max(dim=-1, keepdim=True)[0]
x = torch.cat((x1, x2, x3, x4), dim=1)
x = F.relu(self.bn5(self.conv5(x))).view(batch_size, -1, num_points)
return x # (batch_size, emb_dims, num_points)
可以明显发现与原DGCNN不同的地方是: 作者这里每次forward前传时,并没有再对抽象出来的feature寻找knn进行进一步抽象。而是单纯的不断经过MLP。 对比一下该部分原代码:
x = get_graph_feature(x, k=self.k) # (batch_size, 3, num_points) --> (batch_size, 3*2, num_points, k)
x = self.conv1(x) # (batch_size, 3*2, num_points, k) --> (batch_size, 64, num_points, k)
x1 = x.max(dim=-1, keepdim=False)[0] # (batch_size, 64, num_points, k) --> (batch_size, 64, num_points)
x = get_graph_feature(x1, k=self.k) # (batch_size, 64, num_points) --> (batch_size, 64*2, num_points, k)
x = self.conv2(x) # (batch_size, 64*2, num_points, k) --> (batch_size, 64, num_points, k)
x2 = x.max(dim=-1, keepdim=False)[0] # (batch_size, 64, num_points, k) --> (batch_size, 64, num_points)
x = get_graph_feature(x2, k=self.k) # (batch_size, 64, num_points) --> (batch_size, 64*2, num_points, k)
x = self.conv3(x) # (batch_size, 64*2, num_points, k) --> (batch_size, 128, num_points, k)
x3 = x.max(dim=-1, keepdim=False)[0] # (batch_size, 128, num_points, k) --> (batch_size, 128, num_points)
x = get_graph_feature(x3, k=self.k) # (batch_size, 128, num_points) --> (batch_size, 128*2, num_points, k)
x = self.conv4(x) # (batch_size, 128*2, num_points, k) --> (batch_size, 256, num_points, k)
x4 = x.max(dim=-1, keepdim=False) # (batch_size, 256, num_points, k) --> (batch_size, 256, num_points)
x = torch.cat((x1, x2, x3, x4), dim=1) # (batch_size, 64+64+128+256, num_points)
差别十分明显。相当于网络结构中红框的部分消失了:

此处同样存疑,作者在论文里未提及此细节。
用于Match(寻找点对关系)的Module2
基于Attention机制的Transformer
使用Attention机制的初衷在于:我们想让配准变得更加task specify。也就是说,不再独立地关注两个输入点云$X$,$Y$的embedding feature,而是关注$X$,$Y$之间的一些联合特性。于是乎,自然而然的想到了Attention机制。基于attention,设计一个可以捕捉self-attention和conditional attention的模块,用于学习$X,Y$点云之间的某些联合信息。
我们将由上一个Module对两个点云各自独立生成的embedding特征$F_X,F_Y$作为输入,那么就有: $$ \Phi_X = F_X + \phi(F_X,F_Y) $$ $$ \Phi_Y = F_Y + \phi(F_Y,F_X) $$ 其中,$\phi$是Transformer学习得到的映射函数:$\phi: R^{N \times P} \times R^{N \times P} \to R^{N \times P}$.
我们将$\phi$当做一个残差项,基于$F_X,F_Y$的输入顺序,为$F_X,F_Y$提供一个附加的改变项。
Notice we treat $\phi$ as a residual term, providing an additive change to $F_X$ and $F_Y$ depending on the order of its input.
之所以采取将$F_X \to \Phi_X$的Motivation:以一种适应$Y$中点的组织结构(个人理解即输入顺序)的方式改变$X$的Feature embedding。对$F_Y \to \Phi_Y$,动机相同。
The idea here is that the map $F_X \to \Phi_X$ modifies the features associated to the points in X in a fashion that is knowledgeable about the structure of $Y$.
选择Transformer提供的非对称函数作为$\phi$。Transformer由一些堆叠的encoder-decoder组成,是一种解决Seq2Seq问题的经典架构。关于Transformer的更多信息,移步我的另一篇博客《图解Transformer(译)》
此Module中,encoder接收$F_X$并通过self-attention layer和MLP把它编码到其embedding space,而decoder有两个部分组成,第一个部分接收另一个集合$F_Y$, 然后像encoder一样将之编码到embedding space。另一个部分使用co-attention对两个已经映射到embedding space的点云进行处理。 所以输出$\Phi_Y$,$\Phi_Y$既含有$F_X$的信息,又含有$F_Y$的信息。
这里的Motivation是:将两个点云之间的匹配关系问题(match problem)类比为Sq2Sq问题。(点云是在两个输入的点的序列中寻找对应关系,而Sq2Sq问题是在输入句子中寻找单词之间的联系关系)。
为了避免不可微分的hard assignment,我们使用概率角度的一种方式来生成soft map,将一个点云映射到另一个点云。所以,每一个$x_i \in X$都被赋予了一个概率向量:
$$
m(x_i,Y) = softmax(\Phi_y \Phi_{x_i}^T)
$$
在这里,$\Phi_Y \in R^{N \times P}$代表Y经过Attention Module后生成的embedding。而$\Phi_{x_i}$代表矩阵$\Phi_X$的第$i$行。 所以可以将$m(x_i, Y)$ 看做一个将每个$x_i$映射到$Y$中元素的soft pointer。
下面我们关注文中Transformer的实现。其架构为:

class Transformer(nn.Module):
def __init__(self, args):
super(Transformer, self).__init__()
self.emb_dims = args.emb_dims
self.N = args.n_blocks
self.dropout = args.dropout
self.ff_dims = args.ff_dims # Feed_forward Dims
self.n_heads = args.n_heads # Multihead Attention的头数
c = copy.deepcopy()
attn = MultiHeadedAttention(self.n_heads, self.emb_dims)
ff = PositionwiseFeedForward(self.emb_dims, self.ff_dims, self.dropout)
self.model = EncoderDecoder(Encoder(EncoderLayer(self.emb_dims, c(attn), c(ff), self.dropout),self.N),
Decoder(DecoderLayer(self.emb_dims, c(attn), c(attn), c(ff), self.dropout), self.N),
nn.Sequential(),
nn.Sequential(),
nn.Sequential())
def forward(self, *input):
src = input[0] # batch_size, emb_dims, num_points
tgt = input[1]
src = src.transpose(2, 1).contiguous() # batch_size, num_points, emb_dims
tgt = tgt.transpose(2, 1).contiguous()
tgt_embedding = self.model(src, tgt, None, None).transpose(2, 1).contiguous()
src_embedding = self.model(tgt, src, None, None).transpose(2, 1).contiguous()
return src_embedding, tgt_embedding
上述代码是Transformer的实现。看起来有点绕,我们进一步关注其forward函数.
流入Transformer的data: src,tgt: (batch_size, emb_dims, num_points)
经过transopose.contiguous: src,tgt: (batch_size, num_points, emb_dims)
随后将src, tgt传入self.model,得到了tgt_embedding, src_embedding.
关注self.model,在__init__中定义了self.model:
self.model = EncoderDecoder(Encoder(EncoderLayer(self.emb_dims, c(attn), c(ff), self.dropout), self.N),
Decoder(DecoderLayer(self.emb_dims, c(attn), c(attn), c(ff), self.dropout),self.N),
nn.Sequential(),
nn.Sequential(),
nn.Sequential())
self.model 整体是一个EncoderDecoder类。其传入的参数有一个Encoder,一个Decoder,三个Sequential.
而Encoder传入的参数有两个,第一个是EncoderLayer,第二个是self.N。作为第一个参数的EncoderLayer传入了四个参数,分别是self.emb_dims, c(attn), c(ff), self.dropout.
Decoder传入的参数也是两个,第一个是DecoderLayer,第二个是self.N。作为第一个参数的DecoderLayer传入了五个参数,分别是self.emb_dims, c(attn), c(attn), c(ff), self.dropout.
这里的c是copy.deepcopy(),即深拷贝。完全复制一个新的对象,所以这些网络之间参数并不共享。
首先来关注EncoderDecoder类:
class EncoderDecoder(nn.Module):
def __init__(self, encoder, decoder, src_embed, tgt_embed, generator):
super(EncoderDecoder, self).__init__()
self.encoder = encoder
self.decoder = decoder
self.src_embed = src_embed
self.tgt_embed = src_embed
self.generator = generator
def forward(self, src, tgt, src_mask, tgt_mask):
# Take in and process masked src and target sequences
return self.decode(self.encode(src, src_mask), src_mask, tgt, tgt_mask)
def encode(self, src, src_mask):
return self.encoder(self.src_embed(src), src_mask)
def decode(self, memory, src_mask, tgt, tgt_mask):
return self.generator(self.decoder(self.tgt_embed(tgt), memory, src_mask, tgt_mask))
从上述代码可以看出,EncoderDecoder类构造时传入的五个参数分别为: encoder, decoder, src_embed, tgt_embed, generator.
其前传机制forward是self.decode(self.encode(src, src_mask), src_mask, tgt, tgt_mask)。即先将src,src_mask进行encode,将编码后的结果同src_mask, tgt, tgt_mask一同decode。
而encode函数,是这样定义的: self.encoder(self.src_embed(src), src_mask), 即先将src通过src_embed网络,然后根据其mask再通过encoder网络。
而decode函数,是:self.generator(self.decoder(self.tgt_embed(tgt), memory, src_mask, tgt_mask)), 也就是说, tgt先经过tgt_embed网络,然后随memory, src_mask, tgt_mask一同传入decoder网络,decoder网络的输出再流入generator网络。
所以我自己梳理了一下整个EncoderDecoder大概结构如下:

进一步关注Encoder与Decoder:
def clones(module, N):
return nn.ModuleList([copy.deepcopy(module) for _ in range(N)])
class Encoder(nn.Module):
def __init__(self, layer, N):
super(Encoder, self).__init__()
self.layers = clones(layer, N)
self.norm = LayerNorm(layer.size)
def forward(self, x, mask):
for layer in self.layers:
x = layer(x, mask)
return self.norm(x)
从上述代码,可以看出: Encoder在构造时需要传入两个参数,一个为layer, 一个为N。而在构造函数中,通过调用clones方法将传入的layer深复制(deepcopy)了N次,并作为一个ModuleList存储在self.layers成员变量中。
clones方法的执行效果可从下例中窥见:
net = nn.Sequential(nn.Linear(5,7), nn.BatchNorm1d(5))
print('net',net)
net_clones = clones(net, 3)
print('net_clones', net_clones)
其执行结果是:将net复制了3次,装在一个ModuleList中返回。并且值得一提的是,这里是copy.deepcopy(),深复制,所以参数之间不共享。

而LayerNorm定义如下:
class LayerNorm(nn.Module):
def __init__(self, feature, eps=1e-6):
super(LayerNorm, self).__init__()
self.a_2 = nn.Parameter(torch.ones(features))
self.b_2 = nn.Parameter(torch.zeros(features))
self.eps = eps
def forward(self, x):
mean = x.mean(-1, keepdim=True) # 最后一维的均值
std = x.std(-1, keepdim=True) # 最后一维的标准差
return self.a_2 * (x - mean) / (std + self.eps) + self.b_2 # 对最后一维进行Norm
可见LayerNorm的作用是对输入的数据x,对其最后一维进行归一化操作。
而Encoder整个的前传机制为:对于构造时生成的ModuleList,依次将x通过ModuleList中的每个网络layer,即x = layer(x, mask), 然后再将输出通过LayerNorm对最后一维进行归一化操作返回。 Encoder的网络结构图如下:

进一步关注,Encoder在EncoderDecoder构造时,传入的layer参数为:EncoderLayer(self.emb_dims, c(attn), c(ff), self.dropout)。 解读EncoderLayer:
class EncoderLayer(nn.Module):
def __init__(self, size, self_attn, feed_forward, dropout):
super(EncoderLayer, self).__init__()
self.self_attn = self_attn
self.feed_forward = feed_forward
self.sublayer = clones(SublayerConnection(size, dropout), 2)
self.size = size
def forward(self, x, mask):
x = self.sublayer[0](x, lambda x: self.self_attn(x, x, x, mask))
return self.sublayer[1](x, self.feedforward)
EncoderLayer在构造时需要传入的参数有:size, self_attn, feed_forward, dropout。 其中self_attn, feed_forward两个网络,以及size作为成员变量存储。而另一个成员变量sublayer通过clones方法将SublayerConnection(size, dropout)复制两遍,存着一个ModuleList.
观察SublayerConnection:
class SublayerConnection(nn.Module):
def __init__(self, size, dropout = None):
super(SublayerConnection, self).__init__()
self.norm = LayerNorm(size)
def forward(self, x, sublayer):
return x + sublayer(self.norm(x))
SublayerConnection在构造时,只传入了size, dropout两个参数,用于构造LayerNorm。而前传forward的时候,返回的是x + sublayer(self.norm(x)), 即将x通过了LayerNorm后,再通过作为参数传入的网络sublayer,最后与x相加,返回。
搞清楚SublayerConnection的机制后,我们回看EncoderLayer的forward机制:x先通过一个传入网络为attn的sublayer,然后再通过一个传入网络为feedforward的sublayer. EncoderLayer网络结构如图:

接下来关注attn,即MultiHeadedAttention:
def attention(query, key, value, mask=None, dropout=None):
d_k = query.size(-1)
scores = torch.matmul(query, key.transpose(-2, -1).contiguous()) / math.sqrt(d_k) # (nbatches, h, num_points, num_points)
if mask is not None:
scores = scores.masked_fill(mask == 0, -1e9)
p_attn = F.softmax(scores, dim=-1) # (nbatches, h, num_points, num_points)
return torch.matmul(p_attn, value), p_attn
class MultiHeadedAttention(nn.Module):
def __init__(self, h, d_model, dropout = 0.1):
# h: number of heads ; d_model: dims of model(emb_dims)
super(MultiHeadedAttention, self).__init__()
assert d_model % h == 0
# we assume d_v always equals d_k
self.d_k = d_model // h # d_k 是每个head的dim
self.h = h
self.linears = clones(nn.Linear(d_model, d_model), 4)
self.attn = None
self.dropout = None
def forward(self, query, key, value, mask=None):
if mask is not None:
# Same mask applied to all h heads
mask = mask.unsqueeze(1)
nbatches = query.size(0)
# 1) Do all the linear projections in batch from d_model => h x d_k
query, key, value = [l(x).view(nbatches, -1, self.h, self.d_k).transpose(1, 2).contiguous() for l,x in zip(self.linears, (query, key, value))] # (nbatches, h, num_points, d_k)
# 2) Apply attention on all the projected vectors in batch.
x, self.attn = attention(query, key, value, mask = mask, dropout= self.dropout)
# 3) "Concat" using a view and apply a final linear.
x = x.transpose(1, 2).contiguous().view(nbatches, -1, self.h * self.d_k)
return self.linears[-1](x)
MultiHeadAttention其构造函数有两个参数:h, d_model. 其中h是head的个数,而d_model实际上就是emb_dims。我们总是规定emb_dims是可以整除h的,否则每个attention的维度不是整数。d_k = d_model // h即是每个head的维度。同时在构造时,在self.linears中存储了一个ModuleList,ModuleList中有四个Linear线性映射d_model --> d_model。
MultiHeadAttention的前传机制:
(1) 通过线性映射linear projection,生成query, key, value.
用zip方法将三个线性映射绑定到query, key, value上,相当于指定了其生成的矩阵。(这里的query, key, value只是用于生成query, key, value的原始数据,事实上都是x)。 将query, key, value分别通过对应的Linear Projection投影生成真正的query, key, value。 输入的x的shape是nbatches, num_points, emb_dims (emb_dim 即 d_model). 经过对应的Linear Projection后,生成的shape是nbatches, num_points, emb_dims, 通过view()变为nbatches, num_points, self.h, self.d_k。 随后又进行了transpose(1,2).contiguous(), 那么最后生成的query, key, value的shape是nbatches, self.h, num_points, self.d_k.
需要说明的是,按照Transformer的理论,MultiHeadAttention的生成矩阵(即我们在上面用的投影应该是每个head有一个单独的projection),但是因为这个projection是学习得到的,所以我们只用一个projection然后再进行view()分割得到MultiHead,在理论上应该能得到相同的效果。
(2) 根据得到的query, key, value计算Self-Attention.
Self-Attention的计算: $softmax(\frac{Q \times K^T}{\sqrt{d_k}}) V$

返回的z的shape为:nbatches, self.h, num_points, self.d_k
(3) 通过view进行所谓的Concatenate,将之应用于Linear网络,输出。
首先进行一个transpose(1,2),随后改变其内存分布contiguous,然后再通过view(),相当于把多个头的attention拼接起来。此时的shape为:nbatches, num_points, h * d_k.
再应用于第四个Linear上,输出的shape: (nbatches, num_points, d_model)
整个Attention的网络结构如下:

下面关注PositionwiseFeedForward网络结构:
class PositionwiseFeedForward(nn.Module):
def __init__(self, d_model, d_ff, dropout = 0.1):
super(PositionwiseFeedForward, self).__init__()
self.w_1 = nn.Linear(d_model, d_ff)
self.norm = nn.Sequential()
self.w_2 = nn.Linear(d_ff, d_model)
self.dropout = None
def forward(self, x):
x = F.relu(self.w_1(x)).transpose(2,1).contiguous()
x = self.norm(x).transpose(2,1).contiguous()
x = self.w_2(x)
return x
PositionwistFeedForward的网络结构比较简单,不再单独分析。
整个Encoder的结构分析完毕。 下面再关注一下Decoder:
class Decoder(nn.Module):
def __init__(self, layer, N):
super(Decoder, self).__init__()
self.layers = clones(layer, N)
self.norm = LayerNorm(layer.size)
def forward(self, x, memory, src_mask, tgt_mask):
for layer in self.layers:
x = layer(x, memory, src_mask, tgt_mask)
return self.norm(x)
class DecoderLayer(nn.Module):
# Decoder is made of self-attn, src-attn, and feed forward(defined below)
def __init__(self, size, self_attn, src_attn, feed_forward, dropout):
super(DecoderLayer, self).__init__()
self.size = size
self.self_attn = self_attn
self.src_attn = src_attn
self.feed_forward = feed_forward
self.sublayer = clones(SublayerConnection(size, dropout), 3)
def forward(self, x, memory, src_mask, tgt_mask):
m = memory
x = self.sublayer[0](x, lambda x: self.self_attn(x,x,x,tgt_mask))
x = self.sublayer[1](x, lambda x: self.src_attn(x,m,m,src_mask))
return self.sublayer[2](x, self.feed_forward)
Decoder的网络结构如图:

而DecoderLayer,接收的变量有x,memory,src_mask,tgt_mask,相当于先计算self-attention,再计算co-attention,最后feed-forward,其网络结构为:

至此Transformer应该已经分析清楚了。
用于SVD求解的模块Module3
我们的最终目的是求出刚体变换矩阵。使用上一个Module中计算出的soft pointer,可以生成一个平均意义上的match point。
$$
\hat{y_i} = (Y_m)^T m(x_i,Y)
$$
这里,$Y_m$是指一个$R^{N \times 3}$的矩阵,包含着$Y$中所有点的信息。 根据这样一种match关系,便可以通过SVD求解出刚体变换矩阵。
为了能够使得梯度反向传播,我们必须对SVD进行求导,由于我们使用SVD求解的只是3x3,可以使用其导数的近似形式。SVD求导的详细请参考论文:
Estimating the jacobian of the singular value decomposition: Theory and applications
class SVDHead(nn.Module):
def __init__(self, args):
super(SVDHead, self).__init__()
self.emb_dims = args.emb_dims
self.reflect = nn.Parameter(torch.eye(3), requires_grad=False)
self.reflect[2, 2] = -1
def forward(self, *input):
src_embedding = input[0]
tgt_embedding = input[1]
src = input[2]
tgt = input[3]
batch_size = src.size(0)
d_k = src_embedding.size(1)
scores = torch.matmul(src_embedding.transpose(2, 1).contiguous(), tgt_embedding) / math.sqrt(d_k)
scores = torch.softmax(scores, dim=2)
src_corr = torch.matmul(tgt, scores.transpose(2, 1).contiguous())
src_centered = src - src_mean(dim=2, keepdim=True)
src_corr_centered = src_corr - src_corr.mean(dim=2, keepdim = True)
H = torch.matmul(src_centered, src_corr_centered.transpose(2,1).contiguous())
U,S,V = [],[],[]
R = []
for i in range(src.size(0)):
u, s, v = torch.svd(H[i])
r = torch.matmul(v, u.transpose(1, 0).contiguous())
r_det = torch.det(r)
if r_det < 0:
u, s, v = torch.svd(H[i])
v = torch.matmul(v, self.reflect)
r = torch.matmul(v, u.transpose(1, 0).contiguous())
R.append(r)
U.append(u)
S.append(s)
V.append(v)
U = torch.stack(U, dim=0)
V = torch.stack(V, dim=0)
S = torch.stack(S, dim=0)
R = torch.stack(R, dim=0)
t = torch.matmul(-R, src.mean(dim=2, keepdim = True)) + src_corr.mean(dim=2, keepdim=True)
return R, t.view(batch_size, 3)
疑惑: 没在源码中看到有针对SVD求导的优化。
损失函数
$$ Loss = ||R_{XY}^TR_{XY}^g - I||^2 + ||t_{XY} - t_{XY}^g||^2 + \lambda||\theta||^2 $$
关于DCP_v1和DCP_v2
DCP_v1 没有应用Attention机制。
DCP_v2 应用了Attention机制。
深入探究
关于特征提取:选择PointNet还是DGCNN?
PointNet 学习的是全局特征, 而DGCNN通过构建k-NN Graph学习到的是局部集合特征。
从文中的实验结果可以看出,使用DGCNN作为emb_net,比PointNet的性能始终要好。

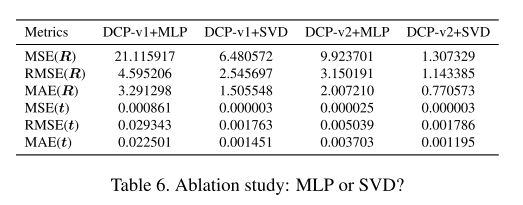
关于计算刚体变换:选择MLP还是SVD?
MLP在理论上可以模拟任何非线性映射。 而SVD是针对任务进行有目的性设计的网络。
从文中的实验结果可以看出,使用SVD计算rigid transformation总是更优。
结语
以上就是我个人对DCP的笔记记录以及一些解读。
疑惑: LayerNorm的作用机制如何?
DCP的缺点
DCP 的文章主要有如下问题:
- 实验进行的数据集是ModelNet40, ModelNet40严格上来讲适用于分类任务,所有点基本都是均匀采样的,没有离群点, 即使有噪声也是人为添加的高斯噪声,这就使得文章的结论很缺乏说服力。
- DCP没有涉及裁剪率的问题,只能对默认两个点云之间是满射,这是不对的。在应用中也会有很多问题。
如果觉得文章对您有帮助,欢迎点赞留言交流。给作者买杯咖啡就更感激不过了!
