0. Abstract

从三维点云或者扫描帧中提取出几何特征是许多任务例如配准，场景重建等的第一步。现有的领先的方法都是将low-level的特征作为输入，或者在有限的感受野上提取得到基于patch的特征。本文提出的是一个全卷积几何特征提取网络，名为fully-convolutional geometric features。 通过一个3D的全卷积网络的一次pass，即可得到几何特征。 同时提出了一个新的度量学习的loss函数，可以显著的提高网络的性能。 FCGF的几何特征十分紧凑，可以捕捉广阔的上下文空间，并缩放到大型场景中。在室内（3D Match）和室外（KITTI）数据集上进行验证的结果显示，其达到了state-of-art的精确率，而且并不需要数据的预处理，并且很紧凑（32维的特征），比其余最精确的方法快290倍。

1. Introduction

寻找几何意义上的点对关系是很多三维任务十分重要的一步。因此，大量的工作集中于设计三维特征，以捕捉具有可判别性的局部几何机构，来建立点对关系。

基于学习的三维特征由于其鲁棒性与出色的性能表现，在最近得到了广泛的关注。现有的基于学习的特征提取工作大都依赖于低阶的几何特征作为输入，例如角度偏差，点的分布，或者体积距离函数等。随后，对每个兴趣点(point of interest)提取一个三维patch，然后通过多层感知机或者三维卷积层将之映射到一个低维的特征空间。 这个过程计算代价高昂，而且只能够提取得到降采样后兴趣点处的特征，因此会降低后续配准步骤中的空间分辨率。

上述的基于patch的处理过程效率很低，因为其中间网络的激活结果并没有在相邻的patch上进行复用。用2D卷积进行类比，对某个兴趣点提取其三维patch与对某个像素块提取其周围的一个像素patch类似。不仅如此，现有的pipeline仅局限于对空间范围有限的patch进行卷积，限制了空间语境的解读。

不同于上文所述，我们应用一个可以作用于整个输入的三维卷积操作，而不需要裁剪片段，该操作是通过将卷积转换为全卷积的子项来完成的（convolution组装得到一个fully convolution）。 相似的，我们将MLP中的全连接层用一系列卷积层来替代，其卷积核的size为1x1x1。 全卷积网络与非全卷积网络相比，可以捕捉更广阔的上下文，更快，内存效率更高。其原因在于中间的激活结果在重叠的区域上进行了复用。

尽管有这些优势，全卷积网络因为三维数据的(一些)特点并未在三维特征提取中得到广泛的应用。一个对三维数据进行卷积的卷积网络的标准输入代表是一个稠密的四维tensor，其中三维是空间维度，还有一个特征维。这种表示方式对内存消耗很大，很多voxel都是空的。

在本文的工作中，采用了一种稀疏的tensor表示法。同时，针对全卷积上的度量学习，提出了一个新的loss函数。因为观察到全卷积特征不同于传统的度量学习的假设，传统的度量学习由于锚点都是随机采样的，所以假设样本是独立同分布的，而在全卷积网络中，相邻的点的特征是高度相关的。并不符合独立同分布的假设，所以需要重新设计loss函数。同时，该方法并不需要对数据进行低阶的预处理，或者提取三维patch，可以快速的生成高分辨率的， 具有state-of-art的判别潜力的特征。

FCGF在室内室外数据集上均进行了测试，可以达到state-of-art的性能表现，比最快的快9倍，比最好的快290倍。

2. Related Work

Hand-craft 3D feature：早期对三维特征的描述集中在手工的，能够有区别的（有基于feature鉴别的潜力 discriminatively）的对局部几何特征进行刻画的描述符。Spin Images [16] use a projection of adjacent points onto the tangent plane. USC [29] uses covariance matrices of point pairs. SHOT [26] creates a 3D histogram of normal vectors. PFH [24] and FPFH [23] build an oriented histogram using pairwise geometric properties. Guo et al. [13] provide a comprehensive review of such hand-crafted descriptors

Learning-based 3D feature： 最近，注意力大都转移到了基于学习的三维特征提取。Zeng et al. [36] use a siamese convolutional network to learn 3D patch de- scriptors. Khoury et al. [17] map 3D oriented histograms to a low-dimensional feature space using multi-layer per- ceptrons. Deng et al. [7, 6] adapt the PointNet architecture for geometric feature description. Yew and Lee [34] use a PointNet to extract features in outdoor scenes.

我们的工作指出了一系列先前工作的局限性。首先，所有先前的方法都需要提取一个小的三维patch，或者一系列点，然后将其映射到低维特征空间，这不但限制了网络的感受野，也使得计算效率很低。甚至是在有重叠的三维区域上，所有中间的表示都需要分别计算。 其次，使用了昂贵的低阶几何特征作为输入，会降低特征计算的速度。 最后， 将特征提取限制在一个兴趣点的子集中，降低了空间的分辨率，会降低后续工作的精确度。

Fully-convolutional networks: 全卷积网络是由Long在图像领域中提出的。三维领域中常被用于语义分割。全卷积网络的广泛应用主要源于其三个优势：首先，全卷积网络效率很高，计算速度快，因为中间激活结果可以在感受野有重叠的神经元上共享。其次，全卷积网络中的神经元有着更加广阔的感受野，因为其不再被限制在分别提取和处理过的patch上。第三点，全卷积网络的输出是稠密的。非常适合需要对场景进行详细描述的任务。

Deep metric learning: 深度度量学习结合了深度神经网络和传统的度量学习，来生成紧凑的embedding。The contrastive loss formulates the objective in terms of pairwise constraints [14]. There has also been significant interest in higher-order loss terms, including triplet [32], quadruplet [18], and histogram losses [30]. Due to the polynomial growth in complexity that accompanies high-order losses, many recent papers focus on triplets with hard-negative mining within a batch. Lifted structure [28] and N-pair losses [27] proposed using a softmax for mining hard negatives within a batch.

在本文中，我们研究了全卷积度量学习，其基本的立足点是： 一个batch内特征是独立同分布的假设不再成立。为了解决这一问题，提出了新的loss函数。

3. Sparse Tensors and Convolutions

空间中的三维点云数据往往是稀疏的，我们使用稀疏矩阵的高阶等价形式–稀疏张量。数学上，我们可以将三维数据的稀疏张量表示为坐标$C$和相关特征$F$的集合： $$ C=\left[\begin{array}{cccc} x_{1} & y_{1} & z_{1} & b_{1} \
\vdots & \vdots & \vdots & \vdots \
x_{N} & y_{N} & z_{N} & b_{N} \end{array}\right], F=\left[\begin{array}{c} \mathbf{f}_{1}^{T} \
\vdots \
\mathbf{f}_{N}^{T} \end{array}\right] \tag{1} $$

其中$x_{i}, y_{i}, z_{i} \in \mathbb{Z}$是第i个三维坐标, $b_i$是batch的索引，为batch processing 提供了一个额外的维度，$\mathbf{f_i}$是与第i个点相关的特征。

在稀疏张量上进行卷积需要一种与传统卷积不同的定义。在离散，稠密的三维卷积(discrete, dense convolution)中，我们提取输入特征然后与dense kernel matrix相乘。用$\mathcal{V}^{n}(K)$表示n维空间中的一组偏移量，其中$K$是核尺寸。例如，在一维卷积中，$\mathcal{V}^1(3) = {-1, 0, 1}$. 那么传统的稠密离散的三维卷积可以被定义为Eq.2，其中$W_i$代表在偏移$i$处的kernel value. $$ \mathbf{x}{\mathbf{u}}^{\text {out }}=\sum{\mathbf{i} \in \mathcal{V}^{3}(K)} W_{\mathbf{i}} \mathbf{x}_{\mathbf{u}+\mathbf{i}}^{\text {in }} \text { for } \mathbf{u} \in \mathbb{Z}^{3} \tag{2} $$

这个公式乍一看可能有点懵，但实际上十分简单，$\mathbf{u} \in \mathbb{Z}^3$是欲求得特征的点的三维坐标，因为并不是在实数域上，所以是离散的(discrete)，但在每个可能位置都可以卷积，所以又是稠密的。 而$\mathbf{i} \in \mathcal{V}^3(K)$是三维意义上的偏离量，$\mathbf{i}$的可能取值例如有：(1,1,1), (1,0,1)等等。 而$\mathbf{u} + \mathbf{i}$就代表了偏移后的坐标，$\mathbf{x}_{\mathbf{u}+\mathbf{i}}^{\text{in}}$是在该偏移坐标上的输入（可能是坐标，也可能是一些低阶特征），乘以对应的kernel value，然后Sum起来，就完成了卷积操作。

但与相反，稀疏张量在$\mathbf{u}$处可以求得特征，当且仅当其对应点即$\mathbf{u} + \mathbf{i}$在集合$C$中。因此，只在子集$\mathcal{N}^{n}(\mathbf{u}, K, C)=\left{\mathbf{i} \mid \mathbf{i} \in \mathcal{V}^{n}(K), \mathbf{i}+\mathbf{u} \in C\right}$上进行卷积操作就足够了。该集合$\mathcal{N}$是$\mathbf{i}$的集合，$\mathbf{i}$满足既是偏移量，与$\mathbf{u}$相加后又在$C$上有定义。如果想让$C^{\text{in}}$和$C^{\text{out}}$的坐标不同（即输入的稀疏张量指定的点的坐标与想要得到的特征的空间点坐标不同），我们可以这样定义这种泛化意义下的稀疏卷积操作，如Eq.3所示： $$ \mathbf{x}{\mathbf{u}}^{\prime \text { out }}=\sum{\mathbf{i} \in \mathcal{N}^{3}\left(\mathbf{u}, K, C^{\text {in }}\right)} W_{\mathbf{i}} \mathbf{x}_{\mathbf{u}+\mathbf{i}}^{\text {in }} \text { for } \mathbf{u} \in C^{\text {out }} \tag{3} $$

Sparse fully-convolutional features: 全卷积网络纯粹由平移不变操作构成，例如卷积操作和基于元素的非线性操作。相似的，如果我们对一个稀疏张量应用一个稀疏的卷积网络，我们会得到一个稀疏的输出张量。我们将这个输出的张量叫做"fully convolutional features"。 我们使用一个带有skip connection 和 残差模块的UNet架构去提取fully convolutional features. 其架构如下图：

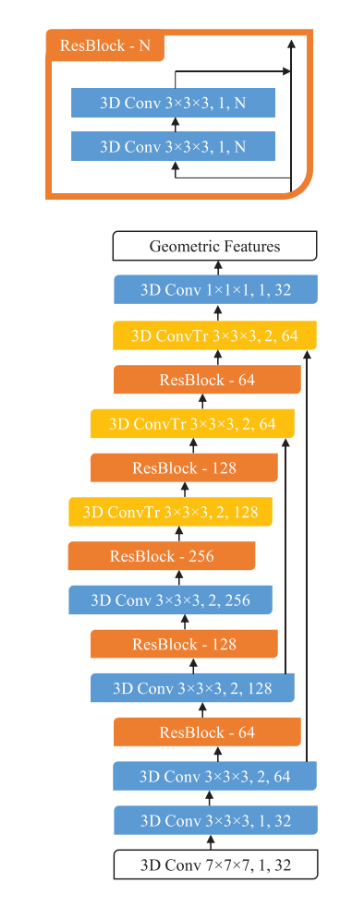
白色块代表着输入和输出层，每个block都由三个参数指定: kernel size, stride, channel dimensionality. 所有的卷积操作（除了最后一层）后都应用了一个batch norm和一个ReLU.

如果对sparse tensor 和 dense tensor以及对应的卷积操作仍有些迷糊，可以看下图：

Dense Tensor and its convolution

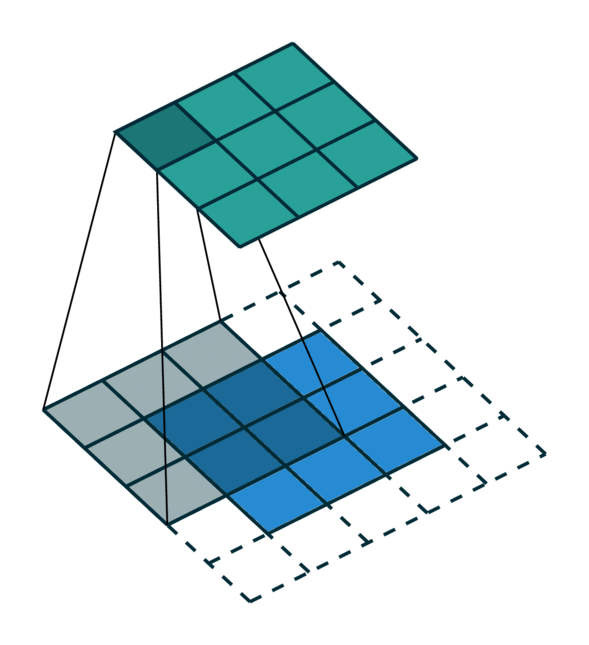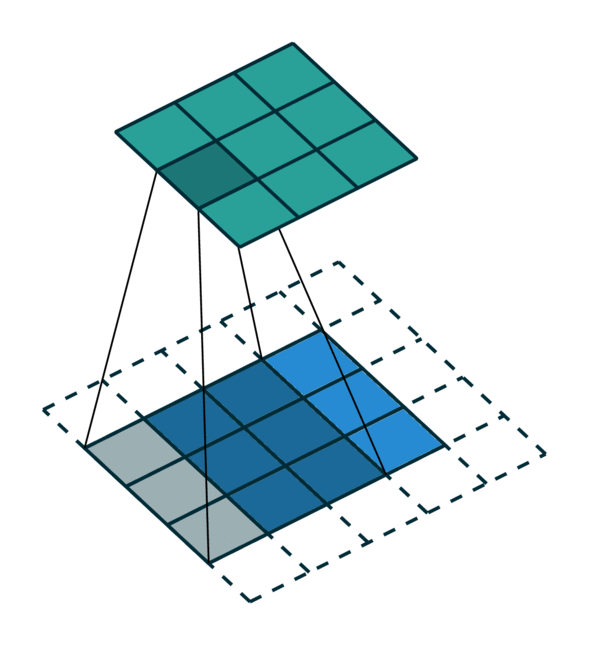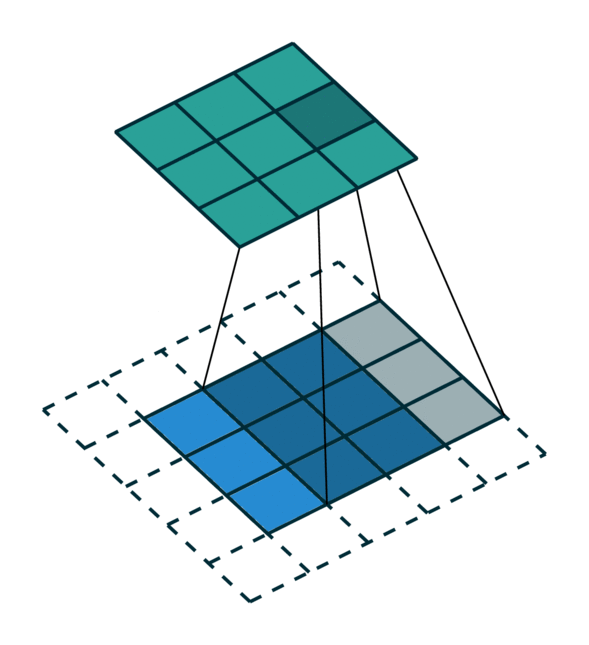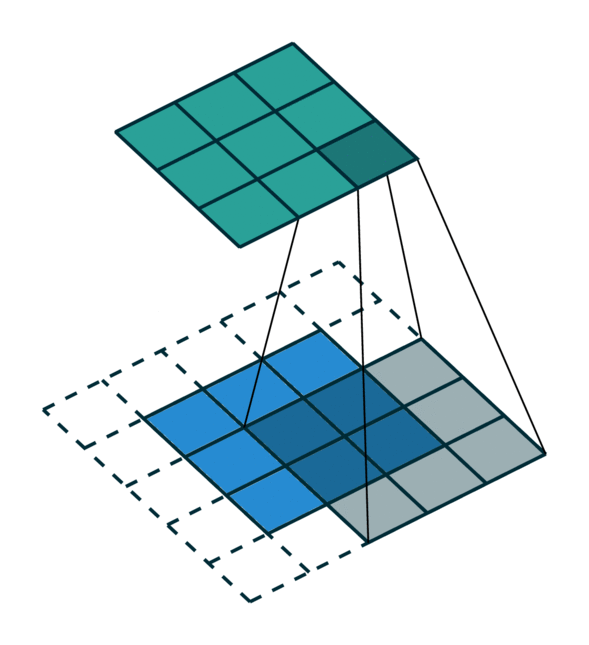
Sparse Tensor and its convolution

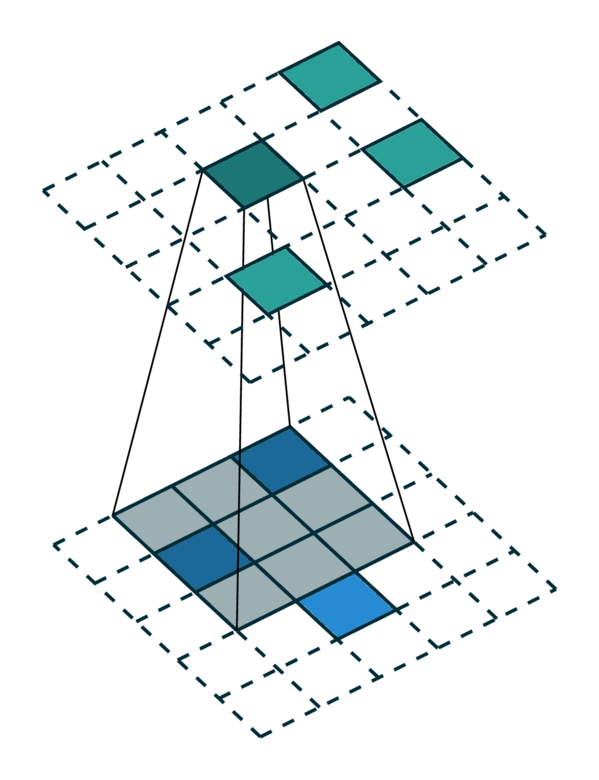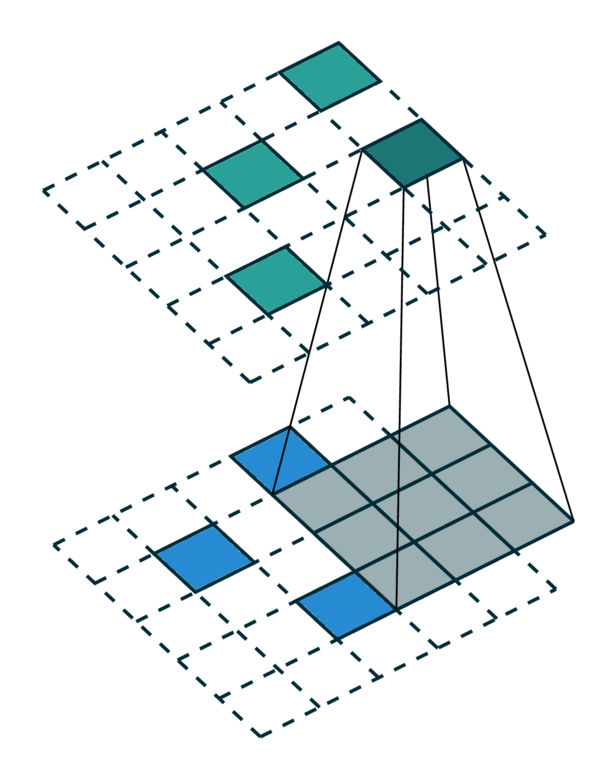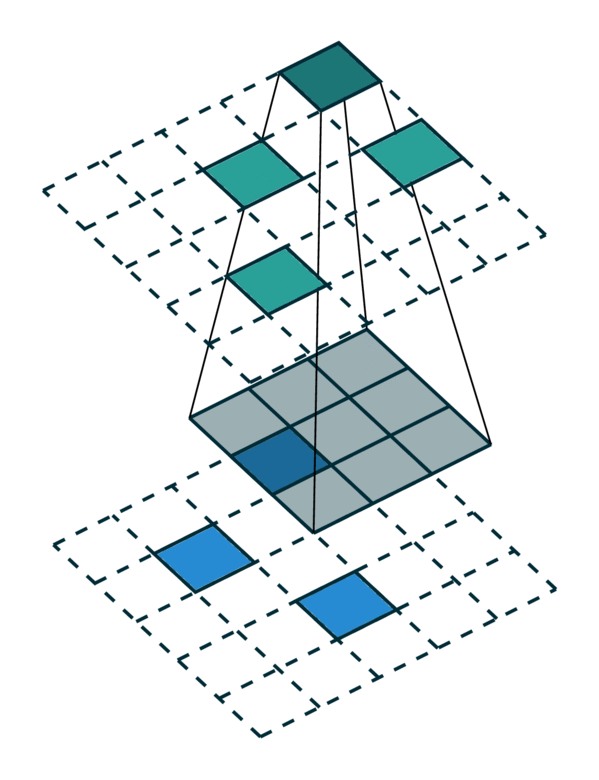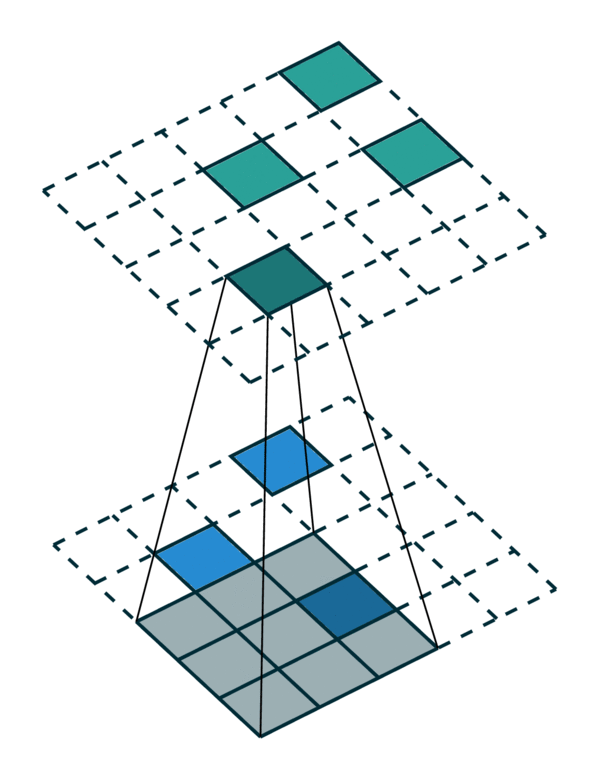
4. Fully-convolutional Metric Learning

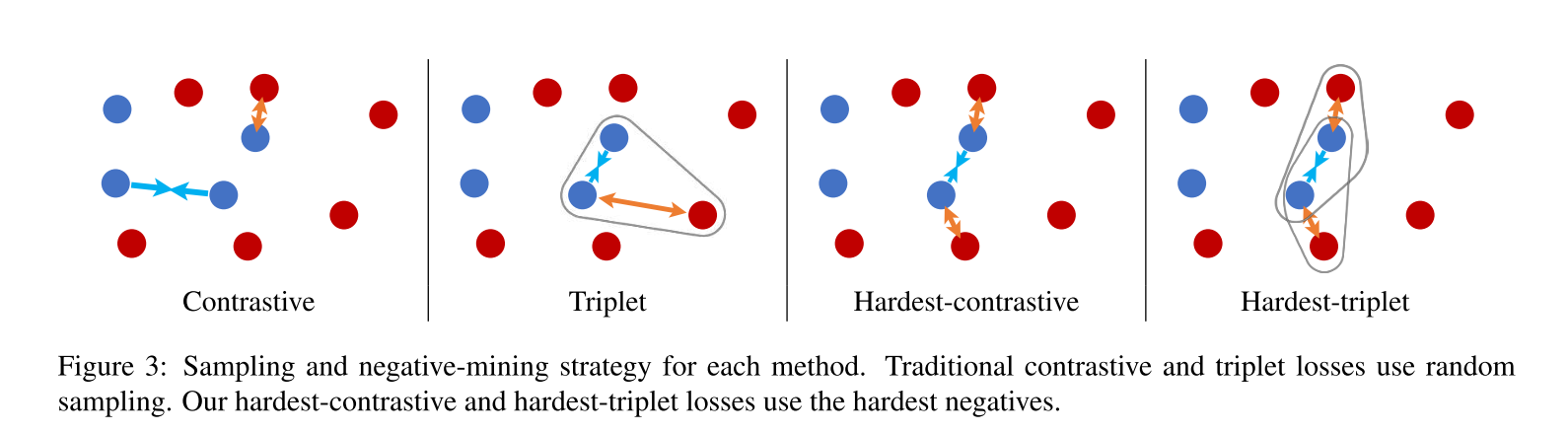
在本节中，我们首先简单回顾一些标准的度量学习损失函数，以及负样本挖掘技术(negative-mining)。随后，我们描述了在全卷积设置下的度量学习，提出了全卷积特征的变种(variants for fully-convolutional features) ， 其将负样本挖掘技术整合于二元误差(contrastive loss)和三元组误差(triplet loss)中。将这种新的loss称为“hardest-contrastive”和"hardest-triplet".

度量学习的出发点有两个约束：相似的feature之间要彼此很近。$D\left(\mathbf{f}{i}, \mathbf{f}{j}\right) \rightarrow 0 \quad \forall(i, j) \in \mathcal{P}$, 而不相似的特征之间的必须要有一个margin以上的距离。$D\left(\mathbf{f}{i}, \mathbf{f}{j}\right)>m \quad \forall(i, j) \in \mathcal{N}$， 其中$D(\cdot, \cdot)$是距离度量函数。将之间的差距进行平方后就能得到一个标准的contrastive loss。但是Lin指出，positive pairs的约束太过严苛，$D\left(\mathbf{f}{i}, \mathbf{f}{j}\right) \rightarrow 0 \quad \forall(i, j) \in \mathcal{P}$，可能会导致过拟合，于是将0也替换为了一个Positive Margin。 $$ L\left(\mathbf{f}{i}, \mathbf{f}{j}\right)=I_{i j}\left[D\left(\mathbf{f}_{i}, \mathbf{f}_{j}\right)-m_{p}\right]_{+}^{2}+\bar{I}_{i j}\left[m_{n}-D\left(\mathbf{f}_{i}, \mathbf{f}_{j}\right)\right]_{+}^{2} $$ 其中当$(i,j) \in \mathcal{P}$ 时，$I_{ij}=1$。 否则为0。 $\bar{\cdot}$ 是逻辑非运算符。$m_p$和$m_n$是positive pair和negative pair的margin。

类似的，我们可以将ranking constraint 即 $m+D\left(\mathbf{f}, \mathbf{f}{+}\right)<D\left(\mathbf{f}, \mathbf{f}{-}\right)$转换为三元组的Loss 函数是： $$ L\left(\mathbf{f}, \mathbf{f}{+}, \mathbf{f}{-}\right)=\left[m+D\left(\mathbf{f}, \mathbf{f}{+}\right)-D\left(\mathbf{f}, \mathbf{f}{-}\right)\right]_{+}^{2} $$

不管是对contrastive loss 还是对 triplet loss， 采样策略都会极大的影响性能，因为判别的边界往往是由几个非常少的难负例决定的。(hardest negatives)

4.1 Characteristics of Fully-convolutional Features

传统的度量学习假定： 特征feature是独立同分布的，因为batch是通过随机采样来构建的。然而，在全卷积特征提取中，相邻的feature之间是局部相关的。因此，难负例挖掘(hard-negative mining)会找到与锚点相邻的特征们，但是他们是假的负例。（难负例的定义是很难判别的负例，所以要再次送入网络进行学习。但是这里锚点相邻的特征是局部相关的，所以其在度量上接近是情有可原的，不是负例。） 所以，将假负例过滤掉是十分重要的，这里采用距离阈值进行过滤。

此外，在全卷积设置下使用的特征数量比标准的度量学习算法中高出若干个数量级。因此，像标准的度量学习那样对batch内的所有成对距离是不可行的。

4.2 Hardest-contrastive 和 Hardest-triplet Losses

在这一节中，我们提出了用于全卷积特征学习的度量学习误差。 像其他的算法一样，我们关注的是有效的难负例挖掘。 首先我们对锚点和每一场景中待挖掘的集合进行采样。随后我们挖掘positive pair $\left(\mathbf{f}{i}, \mathbf{f}{j}\right)$中$\mathbf{f}i$和$\mathbf{f}j$对应的最难负例$\mathbf{f}{i}^{-}, \mathbf{f}{j}^{-}$。同时去除落在对应锚点的一个确定半径中的假负例。 随后，我们对挖掘得到的四元组$\left(\mathbf{f}{i}, \mathbf{f}{j}, \mathbf{f}{i}^{-}, \mathbf{f}{j}^{-}\right)$使用成对损失，得到了convolutional contrastive loss.

$$ \begin{aligned} L_{C} &=\sum_{(i, j) \in \mathcal{P}}\left{\left[D\left(\mathbf{f}_{i}, \mathbf{f}_{j}\right)-m_{p}\right]_{+}^{2} /|\mathcal{P}|\right.\
&+\lambda_{n} I_{i}\left[m_{n}-\min _{k \in \mathcal{N}} D\left(\mathbf{f}_{i}, \mathbf{f}_{k}\right)\right]_{+}^{2} /\left|\mathcal{P}_{i}\right| \
&\left.+\lambda_{n} I_{j}\left[m_{n}-\min _{k \in \mathcal{N}} D\left(\mathbf{f}_{j}, \mathbf{f}_{k}\right)\right]_{+}^{2} /\left|\mathcal{P}_{j}\right|\right} \end{aligned} \tag{5} $$ 其中$\mathcal{P}$是minibatch中在全卷积提取的features上所有的positive pair的集合。而$\mathcal{N}$是minibatch中全卷积feature的一个随机子集，用于负例挖掘。$I_i$是$I(i, k_i, d_t)$的缩写， 是一个指示函数。当特征$k_i$在以特征$i$为中心，$d_t$为半径的球体外时，指示函数取值为1. 反之取0. 其中$k_{i}=\operatorname{argmin}_{k \in \mathcal{N}} D\left(\mathbf{f}_{i}, \mathbf{f}_{k}\right)$， 即$k$是挖掘到的最难的负例。$\left|\mathcal{P}_{i}\right|=\sum_{(i, j) \in \mathcal{P}} I\left(i, k_{i}, d_{t}\right)$是第一项中有效的负挖掘数目。$\left|\mathcal{P}_{j}\right|$是第二项的。通过简单的对所有有效的负例pair等权的进行平均来进行归一化处理。$\lambda_n$是权重。

类似的，带有最难负例挖掘的三元组的loss： $$ \begin{aligned} L_{T} &=\frac{1}{Z} \sum_{(i, j) \in \mathcal{P}}\left(I\left(i, k_{i}\right)\left[m+D\left(\mathbf{f}_{i}, \mathbf{f}_{j}\right)-\min _{k \in \mathcal{N}} D\left(\mathbf{f}_{i}, \mathbf{f}_{k}\right)\right]_{+}\right.\
&\left.+I\left(j, k_{j}\right)\left[m+D\left(\mathbf{f}_{i}, \mathbf{f}_{j}\right)-\min _{k \in \mathcal{N}} D\left(\mathbf{f}_{j}, \mathbf{f}_{k}\right)\right]_{+}\right) \end{aligned} \tag{6} $$ 其中$Z=\sum_{(i, j) \in \mathcal{P}}\left(I\left(i, k_{i}\right)+I\left(j, k_{j}\right)\right)$， 一个归一化常数。 $\mathcal{P}$是batch中在全卷积提取的features上所有的positive pair的集合。 需要注意的是，这里延续了Hermans在其工作中提出的思路，使用了non-squared loss（即误差项没有进行平方）来缓和特征会塌陷于一点的问题。实验中我们发现，fully-convolutional hardest triplet loss会崩溃（所有特征全部收敛到一个点）。所以，我们使用了随机采样的三元组和最难负例挖掘的三元组进行混合的策略，来减小误差。这两项的权重等同。

Code解读

Wait to update