Learning multiview 3D point cloud registration

Abstract

提出了一种全新的，端到端的，可学习的多视角三维点云配准算法。多视角配准往往需要两个阶段：第一个阶段进行初始化配准，给定点云各帧之间两两的初始化刚体变换关系；第二个阶段在全局意义上进行不断精细化处理。前者往往由于点云之间的低重叠率，对称性，或者重复的场景片段而导致配准精度较差。因此，紧随其后的全局优化（Global Refinement）的目标就是在多个点云帧中建立一种循环一致性(cyclic consistency).

而此文章提出了一种算法，将两个阶段融合在一起进行端对端的交替学习。在公认的基准数据集上的实验评估表明，其方法显著优于state-of-art，而且又是端到端可训练的，所需要的计算资源也更少。此外，其还进行了详细的分析和烧蚀试验去验证其方法的novel part.

1. Introduction

三维计算机视觉的下游任务，如语义分割和目标检测，通常需要场景的整体表示。因此，将仅覆盖环境一小部分的单个点云配准和融合为一个全局一致的完整表示的能力是十分重要的，而且在增强现实和机器人技术中有着不少用例。相邻片段之间的双视角配准是一个被深入研究过的问题，传统的基于几何约束[51, 66, 56] 和手工设计的特征描述符[37, 27, 54, 69]的配准方法在某种程度上取得了成功。然而，近些年，用于双视角三维点云配准的局部描述符的研究聚焦于深度学习方法[67: 3DMatch, 38, 21: Ppfnet, 64, 19: Ppf-foldnet, 28: perfect match]，这些方法成功捕捉并编码了隐藏在手工特征符下的证据。在此基础上，一些全新的端到端的双视角点云配准方法最近被提出[62: DCP, 42: Deepvcp]。虽然双视角配准在很多任务中展现出了不错的性能，但对场景中的多个点云帧进行配准时，其存在一些概念上的缺陷：(1) 相邻点云之间的低重合率会导致不精确或者错误的匹配。(2) 点云配准必须依赖于非常局部的特征，对于3D场景结构简单或者重复结构较多的情况十分有害。(3)在两两配准之后，需要进行单独的处理来将所有双视角配准结果组合为一个全局表示。与双视角配准相比，应用于无组织的点云片段上的全局一致的多视角配准方法能够更充分的从深度学习技术取得的进步中获益。现有的领先方法仍然常常依赖于双视角映射的良好初始化（良好的初值），然后再在后续的步骤中通过一系列解耦的步骤进行全局优化。这种分层处理的一大缺点在于，姿态图所有节点上的全局噪声分布在配准结束后远不是随机的。也就是说，由于配准结果和初始的双视角映射高度相关，会存在着不可忽视的误差。

在这篇论文中，作者提出了第一个端到端的，数据驱动的多视角点云配准算法。其方法以可能存在重叠关系的点云集合为输入，对每个点云帧输出一个刚体变换矩阵。我们从传统的两阶段方法中跳脱出来，让各个阶段彼此分离，直接学习以一种全局一致的方式对所有点云帧进行配准。

其工作的主要贡献在于：

将传统的两阶段方法用端到端的神经网络的方式阐述，在其前传过程中，主要解决了两个可微分的最优化问题：(i)对两两点云之间刚体变换参数估计的Procrustes问题。(ii) 刚体变换同步的谱松弛(spectral relaxation)问题
提出了一个置信度估计模块，其使用了一个新颖的overlap pooling layer重叠池化层来预测估算得到的双视角刚体变换参数的可信度。
将多视角三维点云配准问题转换为迭代重加权最小二乘问题(IRLS)，迭代地优化两两配准之间的刚体变换估计和绝对坐标意义下的刚体变换估计（全局）。

因为以上所提到的工作，所提出的多视角点云配准算法是(i) 计算效率很高 (ii) 可以达到更加精确的配准结果，因为残差会以一种迭代的方式被送回双视角配准网络中去。 (iii)不论是双视角配准还是多视角配准，都比现有的方法的精度要高，效果要好。

Pairwise registration: 传统的双视角配准pipeline包含两个阶段： the coarse alignment stage（粗配准），为相对刚体变换参数提供一个初始估计；the refinement stage 通过迭代最小化配准误差，不断优化刚体变换参数。

前者常常通过使用或者手工的，或者学习到的三维局部特征描述符结合类似RANSAC的鲁棒估计或者集合哈希来得到点对之间的对应关系。A parallel stream of works relies on establishing correspodences using the 4-point congruent sets. 在refinement stage，粗糙的刚体变换参数往往通过ICP算法的一个变种提高精度。 ICP类算法通过交替假设点集之间的对应关系和估计其新的刚体变换参数，来达到最优化的目的。但ICP对于离群点不具有鲁棒性，只有在初始的参数估计较好的情况下，才会收敛到全局最优。ICP算法往往通过添加额外的radiometric, temporal or odometry 约束来进行扩展。与我们工作同时进行的，DCP和Dvcp提出了将粗配准和精配准集成的端到端的可学习算法。

Multiview Registration 多视角全局点云配准方法之目标在于通过结合多个视角提供的线索，解决双视角配准应用困难或结果很模糊的情况。第一类方法族使用一种多视角的ICP类模式对位姿和三维点对的对应关系进行优化。其中大多数都受到了增加的点对间对应关系估计复杂性的影响。为了减轻这种影响，有些方法只对运动进行优化，使用扫描来评估配准的误差。更进一步，其他的现代方法利用全局的循环一致性，只对初始时(指定的)点云间两两映射关系的集合进行优化。(通常情况下都是其他帧与第一帧进行配准) 这种有效的方法称之为同步synchronaization。来自运动的全局结构旨在通过分解旋转，平移和缩放变量来同步观测到的相对运动。[23 Deep Mapping]提出了一个使用两个网络进行全局点云配准的方法，一个网络用于位姿估计，另一个通过估计全局坐标的占用状态来对场景结构建模。

或许与此文最相似的工作是[35], 作者旨在通过学习以数据驱动的加权函数来适应刚体变换同步层(transformation synchronization layer)的边缘权值。一个主要的概念上的不同在于其相对刚体变换是通过FPFH结合FGR进行估算而得的，因此不同于本文，本文的刚体变换关系是由学习得到的。此外，在每次迭代中，[35]提出的方法必须将点云转换为一个深度图像，然后再使用一个二维的卷积操作来近似一个权重函数。而本文的方法直接作用于点云，是完全可微分的，所以有助于端到端的多视角全局配准学习。

3. End-to-End Multiview 3D Registration

在这一节中，我们将所提出的多视角三维配准算法作为基于数据的函数的组合进行阐述。而用于近似这些函数的网络架构将在第4节中阐述其细节。我们首先从一个全新的基于学习的双视角点云配准算法开始，其以两个点云作为输入，输出是估计得到的刚体变换矩阵参数。(3.1节) 该方法通过使用一个可反向传播的转换同步层(transformation synchronization)拓展到多点云(3.2)。同步层的输入图作为边缘信息与相对刚体变换参数一起编码为这些成对映射的置信度，该输入图同样是使用一个新的神经网络进行估计得到的。最后，我们提出了一个IRLS模式(3.3)通过更新边的权重和两两点云间的位姿来不断细化全局配准结果。

考虑一个可能存在重叠的点云集合$S = {\bold{S_i} \in \mathbb{R^{N \times 3}}, 1 \leqslant i \leqslant N_S}$. 多视角配准的任务是恢复刚体绝对位姿${ M_i^* \in SE(3)}$，给定了扫描集合，其中：

$$ S E(3)=\left{\mathbf{M} \in \mathbb{R}^{4 \times 4}: \mathbf{M}=\left[\begin{array}{cc} \mathbf{R} & \mathbf{t} \
\mathbf{0}^{\top} & 1 \end{array}\right]\right} \tag{1} $$

$R_i \in SO(3)$ ，$t_i \in \mathbb{R}^3$。 $S$可以通过连接信息表示为一个有限图$\mathcal{G}=(\mathcal{S}, \mathcal{E})$，其中每个点代表着一个单独的点集，边编码了$(i,j) \in \mathcal{E}$ 两个顶点间的相对旋转$R_{ij}$, 平移$t_{ij}$的信息。相对刚体变换参数满足：$R_{ij} = R_{ji}^T$, $t_{ij} = -R_{ij}^Tt_{ji}$，同时还需满足compatibility constraint： $$ R_{ij} \approx R_iR_j^T $$ $$ t_{ij} \approx -R_iR_j^Tt_j + t_i $$

在当前的state-of-art工作中，图G中的边集E是使用一个单独的，辅助的配准算法进行两两配准进行初始化的。而全局场景的一致性是通过后续同步算法来实现的。与之相反，文中提出了一种联合的方法，通过将双视角配准与刚体变换同步紧密耦合为一个完全可微分的组件，提供了一种端到端的，可学习的全局配准pipeline

3.1 Pairwise registration of point clouds (双视角配准)

在本节中，我们提出了一个可微分，双视角配准算法，可以十分轻松地与端到端的多视角三维配准算法结合起来。用${ P,Q} := { S_i, S_j | i \ne j }$表示一对点云，其中$(P)l =: p_l \in \mathbb{R}^3$, $(Q)l =: q_l \in \mathbb{R}^3$分别代表在点云$P \in \mathbb{R}^{N_P \times 3}$和$Q \in \mathbb{R}^{N_Q \times 3}$中的每个点的坐标向量。而双视角配准的目标便是去恢复最优刚体变换矩阵$\hat {R{ij}}$和$\hat t{ij}$. $$ \hat R_{ij}, \hat t_{ij} = \mathop {\arg \min }\limits_{{R_{ij}},{t_{ij}}} \sum\limits_{i = 1}^{{N_P}} {\left| {R_{ij}p_l + t_{ij} - \phi(p_l, Q)} \right|}^2 \tag 3 $$

其中$\phi (p, Q)$是一个对应关系函数，用于将点$p$映射到其在点云$Q$中的对应点。等式（3）中的公式中便于求得一个可微的封闭形式的解，它受噪声分布的影响，接近于真值解。然而，最小二乘解不具有鲁棒性，因此Eq.3往往会在离群点概率高的情况下得到错误的刚体变换参数，在实践中，映射关系$\phi(p, Q)$ 的表现远非理想，错误的对应关系占据了主导地位。为了避免这种情况，等式3可以通过引入一个异方差的加权矩阵来使得其对于离群点具有鲁棒性： $$ \hat R_{ij}, \hat t_{ij} = \mathop {\arg \min }\limits_{{R_{ij}},{t_{ij}}} \sum\limits_{i = 1}^{{N_P}} w_l{\left| {R_{ij}p_l + t_{ij} - \phi(p_l, Q)} \right|}^2 \tag 4 $$

其中$w_l := (\bold{w})_l$是假定的对应关系$\gamma l \in \mathbb{R}^6$所对应的权重，通过一些权重函数$\mathbb{w} = \psi{init}(\Gamma)$计算而得，其中$\Gamma := { \gamma_l } := {P, { \phi(p_l, Q) }l}$, 而$\psi{init} : \mathbb{R} ^{N_P \times 6} \to \mathbb{R}^{N_P}$. 如果假定的对应关系不是离群点，那么权重值$w_l$会接近于1，如果是离群点，那么便接近于0。Eq.4会在保留着可微分的封闭解的基础上得到正确的刚体变换参数。之后我们将这个封闭解表示为加权最小二乘刚体变换(weighted least squares transformation WLS trans).

该可微分的封闭解可通过SVD分解求得。求解过程如下图：

3.2 Differentiable transformation synchronization （可微分的刚体变换同步）

回到多视角配准的任务中来，我们重新考虑给定的初始点云集合$S$。如果提前没有给定任何连接信息（即哪两帧点云之间有边（即配准关系）），图G可以通过指定$\left(\begin{array}{c}N_{\mathcal{S}} \ 2\end{array}\right)$组点云对（即两两之间都有边，类似于全连接），然后利用3.1中所提出的算法来估计其双视角刚体变换参数来进行初始化。全局刚体变换参数可以通过联合(即jointly， transformation synchronization)或独立的方式(将问题拆分为旋转同步(rotation synchronization)和平移同步(translation synchronization))进行估计。在此，我们选择后一种方法，它在谱关系下给出了一个可微的封闭形式的解。

Rotation synchronization: 旋转同步的目标是通过基于其观测到的相对旋转矩阵${ \hat R_{ij} }$ 的比率来解决以下这个最小化问题，来得到全局的旋转矩阵${ R_i^*}$ $$ \mathbf{R}_{i}^{*}=\underset{\mathbf{R}_{\mathbf{i}} \in S O(3)}{\arg \min } \sum_{(i, j) \in \mathcal{E}} c_{i j}\left|\hat{\mathbf{R}}_{i j}-\mathbf{R}_{i} \mathbf{R}_{j}^{T}\right|_{F}^{2} \tag{5} $$ 其中，权重$c_{i j}:=\zeta_{\text {init }}(\boldsymbol{\Gamma})$代表相对刚体变换参数$\hat\bold{M}_{ij}$的置信度。在谱松弛条件下，Eq.5可以得到一个封闭解。

Translation synchronization 相似的，平移同步的目标也是恢复得到全局的平移向量${\mathbf{t}i^*}$，其能够使得下述最小二乘问题得到最小值。 $$ \mathbf{t}{i}^{*}=\underset{\mathbf{t}{\mathbf{i}}}{\arg \min } \sum{(i, j) \in \mathcal{E}} c_{i j}\left|\hat{\mathbf{R}}_{i j} \mathbf{t}_{i}+\hat{\mathbf{t}}_{i j}-\mathbf{t}_{j}\right|^{2} \tag{6} $$ Eq.6也能得到一个可微分的封闭解。

上述的公式(3.1和3.2)在迭代方案中实现起来十分容易，反过来可以将其视为一种IRLS算法。在第k+1次迭代前，我们先通过使用第k次迭代中得到的同步后的相对刚体变换参数$\mathbf{M}{ij}^{*(k)} = \mathbf{M}{i}^{(k)}{\mathbf{M}_{j}^{(k)}}^{-1}$来对点云Q进行预配准:$\mathbf{Q}^{(k+1)}:=\mathbf{M}{i j}^{*(k)} \otimes \mathbf{Q}$ ，其中$\otimes$代表将刚体变换$\mathbf{M}{ij}^{*(k)}$应用于点云$\mathbf{Q}$上。此外，上一次迭代中的权重$\mathbf{w}^{(k)}$和残差$\mathbf{r}^{(k)}$会被当做边缘信息传入对应关系的权重函数(correspondence weighting function)，因此，$\psi_{\text{init}}$便可以被拓展为： $$ \mathbf{w}^{(k+1)}:=\psi_{\text {iter }}\left(\mathbf{\Gamma}^{(k+1)}, \mathbf{w}^{(k)}, \mathbf{r}^{(k)}\right) \tag{7} $$ 其中$\mathbf{\Gamma}^{(k+1)}:={\gamma_{l}^{(k+1)}}:=\left{\mathbf{P},\left{\phi\left(\mathbf{p}_{l}, \mathbf{Q}^{(k+1)}\right)\right}_{l}\right}$

类似的，输入$\hat \mathbf{M}{ij}^{(k)}$ （这里的输入的意思是指在一次迭代中完成了双视角配准，但尚未进行同步，此时会将上一步的结果作为输入传入同步层）和第k次迭代中同步后得到的刚体变换参数$\mathbf{M}{ij}^{*(k)}$的差异也可以作为估计相对刚体变换信息的置信度$c_{ij}^{(k+1)}$的额外线索。因此：$\zeta_{\text{init}}(\cdot)$可以被扩展为： $$ c_{i j}^{(k+1)}:=\zeta_{\text {iter }}\left(\boldsymbol{\Gamma}^{(k+1)}, \hat{\mathbf{M}}_{i j}^{(k)}, \mathbf{M}_{i j}^{*(k)}\right) \tag{8} $$

4.Network Architecture

我们将提出的多视角配准算法实现为了一个深度神经网络，在这一节中，我们首先描述用于近似$\phi(\cdot)$, $\psi_{\text{init}}(\cdot)$, $\psi_{\text{iter}}(\cdot)$, $\zeta_{\text{init}}(\cdot)$和$\zeta_{\text{iter}}(\cdot)$的网络架构。随后再把它们集成为一个完全可微的，端到端的，可训练算法。

4.1 Learned correspondence function

Learned correspondence function: 对对应关系函数$\phi(\cdot)$的近似拓展了一个最近提出的全卷积的三维特征描述子FCGF，和一个软分配层(soft assignment layer)。 FCGF在稀疏的张量上进行操作，通过一次pass，为稀疏点云中的每一个点计算得到一个32维的特征描述子。值得一提的是，我们对$\phi(\cdot)$的模拟可以用任何一个最近提出的基于学习的特征描述网络，如PPFNet等。之所以选择FCGF是由于其具有高准确性，而计算复杂度又很低。

令$\mathbf{F_P},\mathbf{F_Q}$代表点云P，Q经过相同网络权重的FCGF(即shared)后得到的embedding特征。随后，每个点的对应关系${\phi(\cdot)}$可以通过在高维特征空间中的最近邻搜索(NN)而得到。然而，这样一种hard assignment的选择规则不是可微分的。因此我们通过计算一个分类分布的概率向量$\mathbf{s}$，将最近邻选择(NN-selection)以概率的方式进行了re-form. 则点$\mathbf{p}$在点云$\mathbf{Q}$中的推测的对应关系被定义为： $$ \phi(\mathbf{p}, \mathbf{Q}):=\mathbf{s}^{T} \mathbf{Q}, \quad(\mathbf{s}){l}:=\frac{\exp \left(-d{l} / t\right)}{\sum_{l=1}^{N_{\mathbf{Q}}} \exp \left(-d_{l} / t\right)} \tag{9} $$ 其中$d_{l}:=\left|\mathbf{f}_{\mathbf{p}}-\left(\mathbf{F}_{\mathbf{Q}}\right)_{l}\right|_{2}$， $\mathbf{f_p}$是点$\mathbf{p}$的FCGF的embedding，而t表示温度参数(??? temperature parameter)，当t趋近于0时$t \to 0$, $\phi(\mathbf{p},\mathbf{Q})$会收敛于确定的最近邻搜索。

跟随FCGF中的设定，使用对应关系损失$\mathcal{L_c}$来监督$\phi(\cdot)$的学习。损失函数被定义为最严格的对比损失，并应用于FCGF的embedding 上。 $$ \begin{aligned} \mathcal{L}{c}=\frac{1}{N{\text {FCGF }}} & \sum_{(i, j) \in \mathcal{P}}\left{\left[d\left(\mathbf{f}_{i}, \mathbf{f}_{j}\right)-m_{p}\right]_{+}^{2} /|\mathcal{P}|\right.\
&+0.5\left[m_{n}-\min _{k \in \mathcal{N}} d\left(\mathbf{f}_{i}, \mathbf{f}_{k}\right)\right]_{+}^{2} /\left|\mathcal{N}_{i}\right| \
&\left.+0.5\left[m_{n}-\min _{k \in \mathcal{N}} d\left(\mathbf{f}_{j}, \mathbf{f}_{k}\right)\right]_{+}^{2} /\left|\mathcal{N}_{j}\right|\right} \end{aligned} $$ 其中$\mathcal{P}$是FCGF的mini batch $N_{\text{FCGF}}$中所有positive pair的集合，而$\mathcal{N}$是用于最难负例挖掘的随机采样得到的子集。$m_p = 0.1$和$m_n = 1.4$是positive pair 和 negative pair的margin. 关于这个part如果感到困惑的话，可以参考另一篇blog：FCGF论文阅读笔记

$\phi(\cdot)$ 详细的网络结构和训练设置，参数等如下：

网络架构： FCGF特征描述子是在sparse tensor上的。三维数据的稀疏张量表示为坐标$C$和相关特征$F$的集合：

$$ C=\left[\begin{array}{cccc} x_{1} & y_{1} & z_{1} & b_{1} \
\vdots & \vdots & \vdots & \vdots \
x_{N} & y_{N} & z_{N} & b_{N} \end{array}\right], F=\left[\begin{array}{c} \mathbf{f}_{1}^{T} \
\vdots \
\mathbf{f}_{N}^{T} \end{array}\right] \tag{1} $$

其中$x_{i}, y_{i}, z_{i} \in \mathbb{Z}$是第i个三维坐标, $b_i$是batch的索引，为batch processing 提供了一个额外的维度，$\mathbf{f_i}$是与第i个点相关的特征。FCGF是使用Minkowski engine实现的，Minkowski engine是一个auto-differentiation库，它提供了对稀疏卷积的支持，并实现了所有基本的深度学习层。我们采用了FCGF原本的全卷积网络设计，其结构如下图：

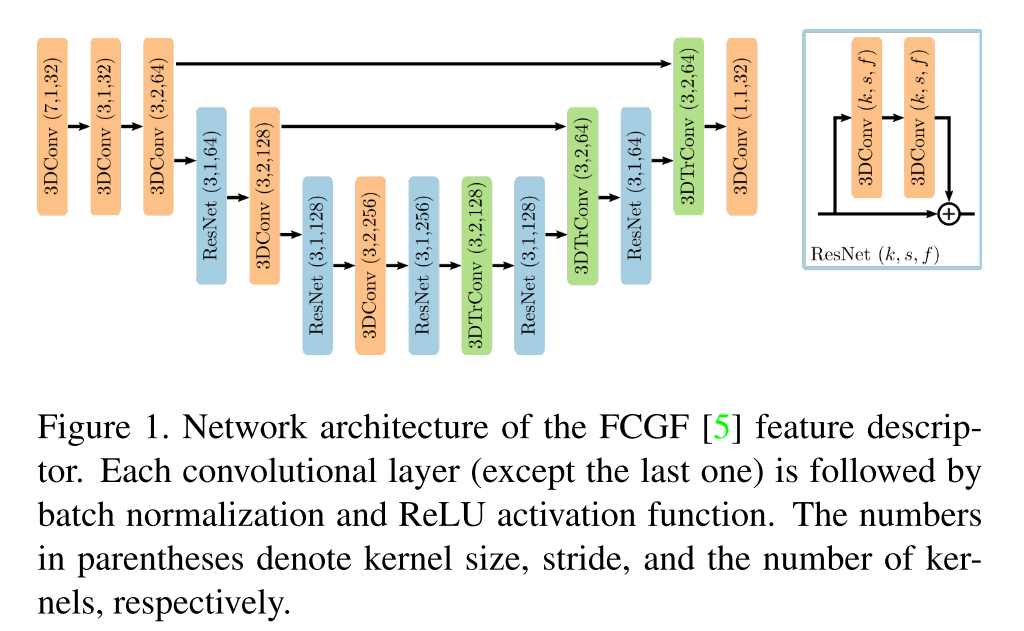
它使用了UNet架构，利用了skip connection 和 ResNet模块为每个点提取一个32维的特征描述子。为了得到独特的坐标$C$，我们使用在GPU上实现的体素网格下采样， voxel size $v := 2.5 \text{cm}$

4.2 Deep pairwise registration

尽管FCGF的特征描述子的性能表现很好，还是会有一些假定的对应关系$\boldsymbol{\Gamma}^{\prime} \subset \boldsymbol{\Gamma}$ 将会是错误的。此外，inliers 和 outliers并不像噪音那样分布，而是呈现出某种规律性。因此我们的目标就是利用深度神经网络学习这种规律性。最近，人们提出了一些网络，用来表示用于过滤二维或三维特征对应关系的复杂权重函数。

在这里，我们提出基于[46: Learning to find good correspondences] 用[68: Learning two-view correspondences and geometry using order-aware network]中的Order-aware block(顺序感知模块)，来扩展3D outlier 过滤网络[29: Robust point-wise correspondences for point cloud based deformation monitoring of natural scenes]. 具体来说，我们创建了一个pairwise的配准模块 $f_{\theta}: \mathbb{R}^{N_{\mathbf{P}} \times 6} \mapsto \mathbb{R}^{N_{\mathbf{P}}}$，其输入是假定的对应关系$\mathbf{\Gamma}$的坐标，输出是权重$\mathbf{w}:=\psi_{\text {init }}(\boldsymbol{\Gamma}):=\tanh \left(\operatorname{ReLU}\left(f_{\theta}(\mathbf{\Gamma})\right)\right)$。随后将权重$\mathbf{w}$与对应关系$\mathbf{\Gamma}$一起, 送入Eq.4的封闭解中去解得$\hat{\mathbf{R}}_{i j}$ 和 $\hat{\mathbf{t}}_{i j}$。受到[53]和[68]的启发，我们在网络中添加了另一个配准模块$\psi_{\text{iter}}(\cdot)$，并将权重$\mathbf{w}$和点对之间的残差$\mathbf{r}$ append到原有的输入中去，服从于：$\mathbf{w}^{(k)} :=\psi_{i t e r}\left(\operatorname{cat}\left(\left[\boldsymbol{\Gamma}^{(k)}, \mathbf{w}^{(k-1)}, \mathbf{r}^{(k-1)}\right]\right)\right)$. 权重$\mathbf{w}^{(k)}$随后再次与初始对应关系$\mathbf{\Gamma}$一同被送入Eq.4的封闭解中，去获得refined 后的双视角刚体变换参数。为了保证$f_{\theta}(\cdot)$的扰动不变性，在每个回归模块中均采用了一种类似PointNet的架构，其对每个单独的对应关系进行操作。因为每个branch只对单独的点对对应关系进行操作，局部的三维上下文信息便通过使用了symmetric context normalization[65] 和 order-aware filtering layers的中间层进行提取。配准模块的详细架构在supplementary里有。 registration network的训练是通过对batch上的$N_{\mathrm{reg}}$个样例定义的配准误差进行监督的： $$ \mathcal{L}_{\mathrm{reg}}=\alpha_{\mathrm{reg}} L_{\mathrm{class}}+\beta_{\mathrm{reg}} L_{\mathrm{trans}} \tag{10} $$

其中$\mathcal{L}{\mathrm{class}}$是普通的二元交叉熵损失函数(此处存疑？？分明不是分类任务，为何在这里用了二元交叉熵损失函数) ，而 $\mathcal{L}{\mathrm{trans}}$则定义如下： $$ \mathcal{L}{\text {trans }}=\frac{1}{N{\text {reg }}} \sum_{(i, j)} \frac{1}{N_{\mathbf{P}}} \sum_{l=1}^{N_{\mathbf{P}}}\left|\hat{\mathbf{M}}_{i j} \otimes \mathbf{p}_{l}-\mathbf{M}_{i j}^{\mathrm{GT}} \otimes \mathbf{p}_{l}\right|_{2} \tag{11} $$

$\mathcal{L}{\mathrm{trans}}$用于惩罚与ground truth的偏移量。$\alpha{\mathrm{reg}}$ 和 $\beta_{\mathrm{reg}}$是用于控制contribution的权重。

4.3 Confidence estimation block

在我们估计得到的相对刚体变换参数$\hat \mathbf{M}{ij}$之间，图$\mathcal{G}$中的边encode了这些估计间的置信度$c{ij}$。图中每个边encode的置信度都由两部分构成：(i) 两两刚体变换估计的局部置信度$c_{ij}^{\mathrm{local}}$. (ii) 从刚体变换同步(transformation synchronization)衍生得到的全局置信度$c_{ij}^{\mathrm{global}}$. 我们将$c_{ij}^{\mathrm{local}}$的估计任务视作一个分类任务，并认为其一些必要的信息包含在在registration block的倒数第二层的特征中。令$\mathbf{X}_{i j}^{\text {conf }}=f_{\theta}^{(-2)}(\cdot)$ 表示registration block中的倒数第二层的输出。我们提出了一个 *overlap pooling layer* 重叠池化层来通过加权平均池化提取全局特征$\mathbf{x}_{i j}^{\mathrm{conf}}$: $$ \mathbf{x}_{i j}^{\mathrm{conf}}=\mathbf{w}_{i j}^{\mathrm{T}} \mathbf{X}_{i j}^{\mathrm{conf}} \tag{12} $$

得到的全局特征与inlier的比率$\delta_{i j}$(即权重比给定阈值高的点对对应关系的数量)进行concatenate。随后送入置信度估计网络，该网络由三个全连接层构成(129-64-32-1)，其后跟随一个ReLU激活函数。所以local confidence局部置信度可以被表示为: $$ c_{i j}^{\text {local }}:=\zeta_{\text {init }}(\boldsymbol{\Gamma}):=\operatorname{MLP}\left(\operatorname{cat}\left(\left[\mathbf{x}_{i j}^{\text {conf }}, \delta_{i j}\right]\right)\right) \tag{13} $$

confidence estimation block置信度估计模块的训练由置信度损失函数(confidence loss function) $\mathcal{L}{\mathrm{conf}} = \frac{1}{N} \sum{(i, j)} \operatorname{BCE}\left(c_{i j}^{\text {local }}, c_{i j}^{\text {GT }}\right)$ 进行监督, 其中BCE指代二元交叉熵，ground truth confidence $c_{i j}^{\mathrm{GT}}$是在运行时，通过控制角度误差的阈值$\tau_{a} = \arccos \left(\frac{\operatorname{Tr}\left(\hat{\mathbf{R}}_{i j}^{T} \mathbf{R}_{i j}^{\mathrm{GT}}\right)-1}{2}\right)$来计算得到的。

在这里反思，原来作者所说的将其当做一个分类问题实质是上是一个二分类问题，$c_{ij}$的取值只有两个，要么是0，要么是1。

$\zeta_{\text {init }}(\cdot)$函数计算得到了相对刚体变换参数的局部置信度。在另一方面，刚体变换同步层的输出(即全局刚体变换信息)提供了输入的相对刚体变换是如何与其他边之间保持全局一致的信息。事实上，传统的同步算法[13,4,24]仅仅使用了其全局信息去在迭代中为每个边重新计算权重，原因在于他们并没有获得局部置信度的途径。相对刚体变换参数的全局置信度$c_{ij}^{\mathrm{global}}$可以被表示为柯西权重函数[33,4]： $$ c_{i j}^{\text {global }}=1 /\left(1+r_{i j}^{*} / b\right) \tag{14} $$ 其中$r_{i j}^{*}=\left|\hat{\mathbf{M}}_{i j}-\mathbf{M}_{i}^{*} \mathbf{M}_{j}^{*^{T}}\right|_{F}$，跟随[33,4]的思想，$b=1.482 \gamma \operatorname{med}\left(\left|\mathbf{r}^{*}-\operatorname{med}\left(\mathbf{r}^{*}\right)\right|\right)$, 而$\mathrm{med}(\cdot)$代表一个平均算子(median operator)。$\mathbf{r}^*$ 是残差$r_{ij}^*$的向量表达形式。此处存疑，$\gamma$ 是啥？是对应关系？那这个怎么能混到实值计算里来呢？由于局部置信度与全局置信度提供了关于相对刚体变换参数的完整信息，我们使用其调和平均数将其结合为一个联合置信度$c_{ij}$: $$ c_{i j}:=\zeta_{i t e r}\left(c_{i j}^{\text {local }}, c_{i j}^{\text {global }}\right):=\frac{\left(1+\beta^{2}\right) c_{i j}^{\text {global }} \cdot c_{i j}^{\text {local }}}{\beta^{2} c_{i j}^{\text {global }}+c_{i j}^{\text {local }}} \tag{15} $$ 其中$\beta$用于平衡局部置信度与全局置信度估计的贡献度，是在训练中学习得到的。

仍存疑，这里与上面$c_{ij}^{\mathrm{local}}$的0,1判断显然矛盾。那么$c_{ij}^{\mathrm{local}}$到底怎么计算的？难道是误差$\tau$与阈值的比值？？

4.4 End-to-end multiview 3D registration

网络中每个独立的part 按照下图所示，连接成为一个端到端的多视角三维配准算法。

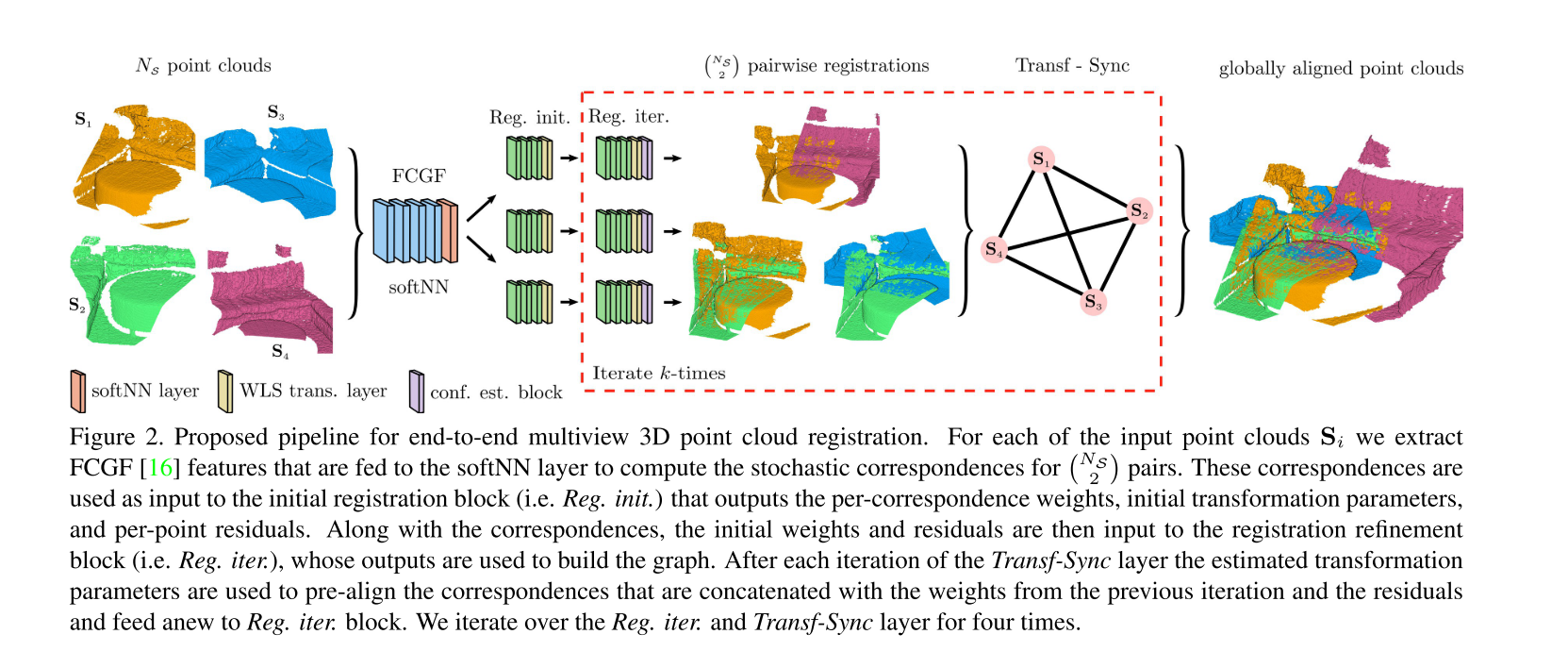
我们先对对每个子网络进行预训练(pretrain)，然后再在3DMatch数据集上以端到端的方式，使用官方的训练测试集划分来微调整个模型。在微调阶段我们使用$N_{\mathrm{FCGF}} = 4$来提取FCGF的特征，并从每个片段中随机采样2048个点的特征向量。这些feature被用于soft NN，来形成假定的$\left(\begin{array}{c}N_{\mathcal{S}} \ 2\end{array}\right)$组点对对应关系，随后被送入双视角配准网络。双视角配准的输出用于构建整个图，随后被输入刚体变换同步层。刚体变换参数迭代求精的过程共进行四次。我们使用联合多视角配准损失函数来对微调过程进行监督学习： $$ \mathcal{L}=\mathcal{L}_{\mathrm{c}}+\mathcal{L}_{\mathrm{reg}}+\mathcal{L}_{\mathrm{conf}}+\mathcal{L}_{\mathrm{sync}} \tag{16} $$

其中刚体变换同步损失函数$\mathcal{L}{\text {sync }}$记做： $$ \mathcal{L}{\text {sync }}=\frac{1}{N} \sum_{(i, j)}\left(\left|\mathbf{R}_{i j}^{*}-\mathbf{R}_{i j}^{G T}\right|_{F}+\left|\mathbf{t}_{i j}^{*}-\mathbf{t}_{i j}^{G T}\right|_{2}\right) \tag{17} $$

我们对网络参数微调的过程共进行了2400次迭代，使用Adam优化器，学习率为$5 \times 10 ^{-6}$