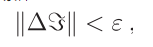MATrICP

论文

Improved techniques for multi-view registration with motion averaging
Li, Zhongyu Zhu, Jihua Lan, Ke Li, Chen Fang, Chaowei

核心思想

将Trimmed ICP与运动平均算法结合起来，应用到多视角聚类上。

算法步骤

1. 估算各帧之间的重叠百分比$\xi_{i,j}$

总的来说，估算各帧之间的重叠百分比主要分为两步：
(1) 对于每一帧，计算其$d_{threshold}$
(2) 计算出每一帧的$d_{threshold}$之后，使用该参数计算该帧与其他帧的重叠百分比。

1.0 背景知识

ObjFunc：

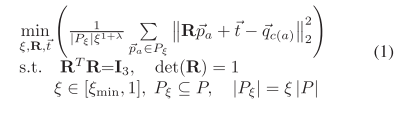
1.1 计算$d_{threshold}$

对于第i帧的每一个点，可以在其他所有帧中寻找到N-1个对应点（通过NN），假设第i帧有$N_i$个点，那么一共会有$N_i * (N-1)$个点对与距离。因为我们是要进行多视角配准的，相当于把当前帧作为源scan，其他所有帧组成的模型作为目标模板进行配准。所以将这些所有距离按照从小到大进行排序，然后依次对于每一个距离，计算该距离以及之前所有距离对应的ObjectFunction值。可以使用cumsum操作。结果是得到同样长度的ObjectFunction值的数组，取其中的最小值，该目标函数最小值对应着一个距离$d_i$，这个距离$d_i$就可以作为第i帧的$d_{threshold}$，用于第i帧与其他帧（第j帧）的重叠率估算。

1.2 计算第i帧与其他帧的重叠百分比

对于第$i$帧，我们现在有其$d_{threshold}$。那么求$\xi_{i,j}$，即为：使用NN寻找点对pair$(P_i,P_j)$，然后从小到大排列，取$d < d_{threshold}$的部分。假设有$N_j^{'}$个点对满足要求。那么重叠百分比$\xi_{i,j} = N_j^{'} / N_j$，$N_j$为第j帧的点。

2. 根据估算得到的${\xi_{i,j}}$，选择重叠率高的scan pair，应用TrICP算法求解其relative Motion $M_{i,j}$

2. 应用运动平均算法

在应用Motion Average前，我们已经有了初始的Global Motion以及一系列Relative Motion。
运动平均的主要思想是，将relative Motion看作是global Motion的某种组合。先求出$\Delta M_{i,j}$，将其转换为李代数对应的6x1的向量。然后通过Average的思想，求出global Motion的变化值。

2.1 计算relative motion $M_{i,j}$的变化值

通过global motion，可以求出$\Delta M_{i,j}$ $$ \Delta M_{i,j} = M_i^0 M_{i,j} {(M_j^0)}^{-1} $$

2.2 转换为李代数，从SE(4) 到 se(4)

$$ \Delta m_{i,j} = logm(\Delta M_{i,j}) $$

2.3 求李代数上变化量的均值

首先先使用映射将其李代数映射为其对应的六元向量： $$ \Delta v_{i,j} = vec(\Delta m_{i,j}) $$

然后构造一个矩阵D，应用如下公式即可求出global motion的Average值。

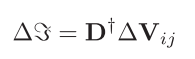
$D_{i,j}$在第i列是$-I$，在第j列为$I$。

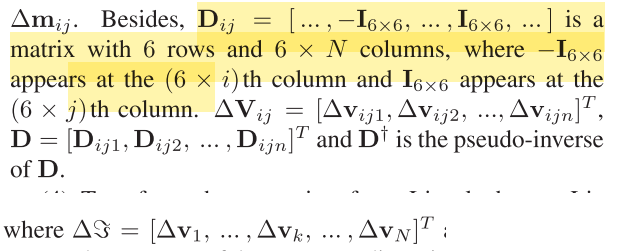
D的含义可能比较难理解，我们有：
$$ \Delta \zeta = D^{\dag} \Delta V_{i,j}
$$ $$ D \Delta \zeta = \Delta V_{i,j} $$ 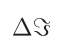该符号打不出来，我们用$\Delta \zeta$代替了。

举个例子： 一共3个scan。relativeMotion有两个，假设为$\Delta v_{1,2}, \Delta v_{1,3}$。

可以看出来，通过D对$\Delta \zeta$的线性变换，的确得到了$\Delta v_{i,j}$的另一种表现形式，所以对D求伪逆，左乘在$V_{i,j}$旁，即可得到包含有global motion的结果。

2.4 根据求得的global motion difference，变换回SE(4)，对现有Motion进行更新。

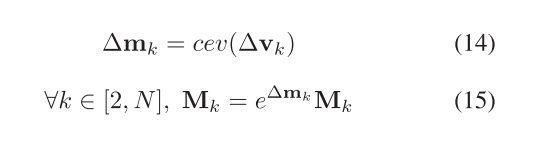
2.5 判断是否满足条件，若不满足重新回到2.1， 若满足退出。

条件：